Hilfe bei geometric Brownian motion in excel

Question

ich bin gerade dabei meine Masterarbeit in Finance zu schreiben.

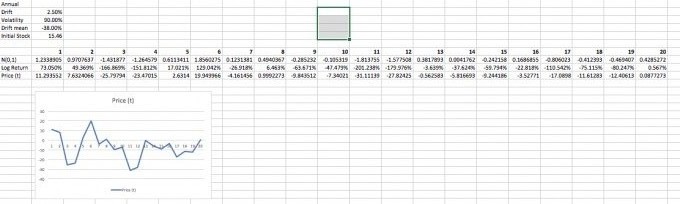
In einem Artikel von der Standford University wird für die Berechnung des Aktienpreises (share price) also der Fair Value (FV) Wert anhand der geometric Brownian motion Methode in Excel berechnet. ich würde es gerne selber machen. Leider bekomme ich die Formel in Excel nicht.

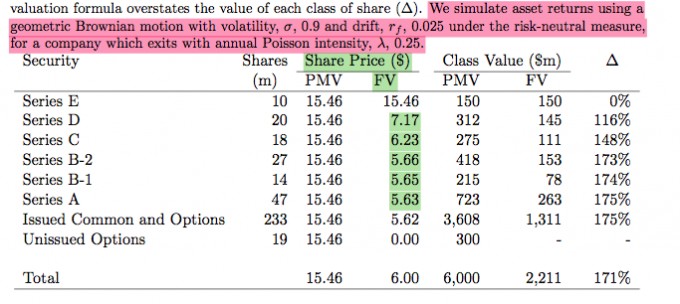
Wie in der Abbildung zu sehen ist, werden die Anlagerenditen mit der geometric Brownian motion Methode berechnet:

dafür werden folgende Daten benutzt:

Volatilität= 0.9

Drift= 0. 0025 (unter der risikoneutralen Messung)

λ= 0.25 (jährliche Poisson Intensität)

Leider weiß ich nicht wie genau ich vorgehen soll.. damit ich diese Fair Value (FV) auch herausbekomme.

Ich habe es selber in Excel versucht, aber es erscheint mir nicht ganz logisch.

Ich wäre euch sehr dankbar für die Hilfe!!

Liebe Grüße

Answer 1

Stanford ist ein Gemäuer und schreibt keine Artikel. Die kommen immer von Autoren. Wie sollen die Leute hier verstehen, was die unbekannten Autoren des unbekannten Artikels in einer unbekannten Zeitschrift gemeint haben, wenn du das alles im Dunkeln lässt? Ein Artikel in dem nicht hinreichend klar steht, was gerechnet wurde, würde gar nicht publiziert.

Answer 2

Hi, reden wir über folgenden Prozess
$$S_t = a e^{ \left(\mu - \frac{ \sigma^2 }{ 2 }\right) t +\sigma W_t }$$
wobei $W_t$ ein Wienerprozess ist?
Wenn ja, $\mu$ und $\sigma$ sind ja bekannt, aber auch $a = S_0$ ?
$W_t$ kann man wie folgt erzeugen
$$W_{n \Delta t } = \sqrt{\Delta t } \sum_{i=1}^n Z_i$$ wobei $Z_i$ unabhängige, standardnormal verteilte Zufallsvariablen sind.

Comments

Eine andere Möglichkeit eine geometrische Bewegung zu simulieren besteht in folgendem Algorithmus

$$S_{i+1} = S_i + \mu S_i \Delta t + \sigma S_i \sqrt{ \Delta t } Z_i$$

Die Ergenisse sind identisch und so sehen sie aus