Wann ist eine Argumentation vollständig?

Question

Der emeritierte Mathematiker Hermann Karcher findet in einem Schulbuch diese Darstellung zur Veranschaulichung des Winkelsummensatzes:

Er schreibt dazu:
In Wahrheit geht Mathematik seit über 2000 Jahren anders. Der hier zu sehende vorsätzliche Verzicht auf logische Argumentation und Mitteilung von Sätzen in Form von Rezepten erweist sich als durchgängiges Prinzip.

In der Mathelounge veröffentlichte hj2166 (auf die Frage nach der Rechteckfläche links in Abhängigkeit von der Länge der roten Strecke) diese Darstellung:


Darauf scheibt ein Mitglied:
Bei diesem schönen Bildchen ist aber noch eine beträchtliche argumentative Lücke zu schließen. Warum ergibt sich ein Quadrat (und nicht nur ein profanes Rechteck)?

In beiden Fällen geht es um die Frage: ‚Müssen in jeder Begründung einer mathematischen Aussage wirklich alle argumentativen Lücken geschlossen sein?‘

Die Antwort fällt für die Schule sicher anders aus als für die Universität. In der Schule geht es in allererster Linie um die Einsicht der Schüler*innen in das ‚Warum‘ der Gültigkeit der Aussage. Zu diesem Zecke sind beide Darstellungen bestens geeignet. Natürlich sollte auch in der Schule die logische Argumentation geübt werden, um die es dann in der Universität geht. Aber selbst dann bleibt die Frage zu klären, wann eine Argumentation als lückenlos zu bewerten ist. Vollständige Lückenlosigkeit wird erst erreicht, wenn alle Hilfsaussagen und Hilfskonstruktionen auf Axiome zurückgeführt wurden. Dies ist in der Schule nicht möglich, da Schulmathematik nicht axiomatisch betrieben wird. Selbst in der Wissenschaft Mathematik ist eine solche vollständige Rückführung nicht üblich. Bei jeder argumentativen Kommunikation ist Verständigung nur auf einer gemeinsamen Grundlage möglich, die stillschweigend vorausgesetzt wird.

Comments

Hallo roland

Ganz verstehe ich deine Aussagen nicht. hältst du das Aneinanderlegen von abgerissenen Ecken eines Dreiecks für eine Art der der Argument für SuS? Niemand hat ja was dagegen, das als Einstieg zu benutzen. Dass auf der Schule das parallelenaxiom benutzt wird (ob Axiom genannt oder nicht) ist bekannt. etwa für Stufen- und Wechselwinkel. was spricht also - nach der Einführung- gegen eine einfache Argumentation? SuS sehen leicht selbst dass man beim Zusammenlegen nicht zwischen 178°18o° und 182° unterscheiden kann. also sag bitte genauer, welche Argumente oder auch welche Axiome= Grundannahmen für dich auf der Schule nötig oder überflüssig sind. Auch Pythagoras kann man aus einem puzzle zusammenlegen trotzdem wird es in JEDEM Schulbuch, das mir bekannt ist echt bewiesen.

lul

---

Hallo lul, du verstehst mich nicht, weil du nicht genügend aufmerksam liest. Vielleicht ist dir aufgefallen: In der Schule tritt die Evidenz an die Stelle mancher Beweise und aller Axiome. Der Wechselwinkelsatz ist entweder evident oder er ergibt ich als Resultat einer Drehung.

Answer 1

Solche Bilder dienen in erster Linie der Veranschaulichung, so dass man schnell Einsicht in die Richtigkeit mathematischer Aussagen bekommt. Das halte ich gerade in der Schule für ausgesprochen wichtig, um auch ein Verständnis von Mathematik greifbarer zu machen. Ein weiteres prominentes Beispiel ist die binomische Formel:

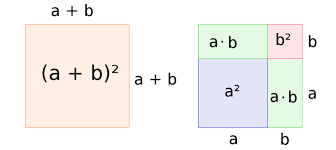
Allerdings gibt es auch Beispiele, die eindrucksvoll zeigen, dass ein Bild eben nicht immer eine ausreichende Argumentation ist, wie dieses sicherlich bekannte Beispiel zeigt:

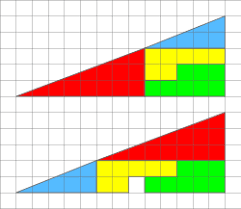
Während das erste Beispiel keine weitere mathematisch formale Argumentation benötigt, kann man sie beim zweiten Beispiel nicht einfach ignorieren. Der scheinbare Widerspruch in diesem Beispiel muss - vor allem für den Laien - mathematisch erklärt werden können (in diesem Zusammenhang kennen sicherlich manche auch das Geheimnis der unendlichen Schokolade).

Bilder zur Veranschaulichung mathematischer Aussagen liefern also in erster Linie eine sofortige Einsicht, können aber natürlich auch Zweifel säen. Daher muss parallel immer auch eine formale Erklärung erfolgen, insbesondere bei Sachverhalten, die nicht sofort offensichtlich sind, wie das Beispiel von hj2166 zeigt, wo sicherlich nicht sofort für jeden die Kongruenz zweier Dreiecke ersichtlich ist.

Comments

Eine sehr schöne und wichtige Ergänzung meines Beitrags.