Welche Maße braucht der Container, wenn der Materialverbrauch minimal sein soll?

Question

Hey zusammen

ein quaderförmiger oben geöffneter Container soll halb so hoch wie breit sein und ein Volumen von 108m^3 besitzen. Bei welchen Maßen ist der Materialverbrauch minimal?

Danke schon jetzt

Answer 1

V = a * b * h = 108
h = b / 2
a * b * b / 2 = 108
a * b^2 = 216
a = 216 / b^2

O = a * b + a * h * 2 + b * h * 2
O = a * b + ( a + b ) * h * 2
O = a * b + ( a + b ) * b / 2  * 2
O = a * b + ( a + b ) * b
O = a * b + a * b + b^2
O = 2 *a * b + b^2
O = 2 * 216 / b^2 + b^2
O = 512 / b^2 + b^2
Ersetzen
x = b^2
O = 512 / x + x
O ´ = -512 / x^2 + 1
Extremwert
-512 / x^2 + 1 = 0
-512 / x^2 = -1
x^2 = 512
x = 22.63 m
Rückersetzen
x = b^2
22.63 = b^2
b = 4.76 m

h = b / 2
h = 2.38 m

a = 216 / b^2
a = 9.54 m

Probe
V = 9.54 * 4.76 * 2.38 = 108 m^3
Stimmt schon einmal.

Bitte alles nachprüfen.

Comments

Zur Diskusion :
ist nicht ein Quadrat die kleinste (Grund-) Fläche
mit dem kleinsten Umfang ?
Dann wären wir schnell fertig.
V = a * a *a/2 = 108
a = 6
b = 6
h = 3
O = 6^2 + 24 * 3 = 36 + 72 = 108

---

Korrektur:
O = 2 *a * b + b²
O = 432 / b * + b²

O ´ ( b ) = - 432 / b^2 + 2 * b
- 432 / b^2 + 2 * b = 0
-432 / b^2 = - 2 b
216 = b^3
b = 6 m

h = b / 2
h = 3 m

a = 216 / b²
a = 6 m

---

vielen dank georgborn, alles klar.

Answer 2

Ich habe die Einheiten absichtlich weggelassen, müssen natürlich geschrieben werden.

                                                             

Answer 3

V= x*y/2*y = x*y^2/2=108

x= 216/y^2

O = x*y/2+2*x*y+2*y/2*y = x*y/2+2x*y+y^2

O(y)= 108y^2+432/y+y^2

Berechne: O '(y)= 0

...

Answer 4

Hallo Julian,

sorry, das Folgende gilt leider nur für einen oben geschlossenen Container.

V = l * b * h,   l = y  , b = x ,  h = x/2

V = x * y * x/2  = 108  | * 2  | : x^2

→   y = 216/x^2

O =  2 * (l*b + l*h + h*b)  = 2 *( 216/x^2 * x + 216/x^2 * x/2 + x/2 * x ) 

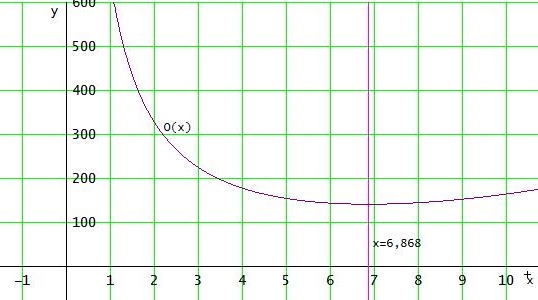
→   O = (x^3 + 648) / x

O ' =  (x^3 + 648) / x  = 0

→  x = 3·12^{1/3}  ≈ x = b  = 6.868

x Einsetzen  →  y = l  ≈  4.579  und   h ≈ 3.434

Gruß Wolfgang

Comments

Hallo Wolfgang,

Fehler ?

In der Fragestellung heißt es
oben geöffneter Container

( die obere Deckplatte fehlt )

Du hast mit oben geschlossenem Container
gerechnet

O =  2 * (l*b + l*h + h*b)

---

Hallo Georg,

Fehler? Ja, habe ich offensichtlich überlesen. Danke für den Hinweis. Lasse es jetzt so stehen, weil es genug andere Antworten gibt.

---

Hallo Wolfgang,
es gibt jetzt genug andere richtige
Antworten für den Fragesteller.
Das sehe ich auch so.

Frage : kann der erfahrene Mathematiker
erkennen :  ich schrieb
ist nicht ein Quadrat die kleinste (Grund-) Fläche
mit dem kleinsten Umfang ?
und kann auf die Maße des Container somit
einfach geschlossen werden ?