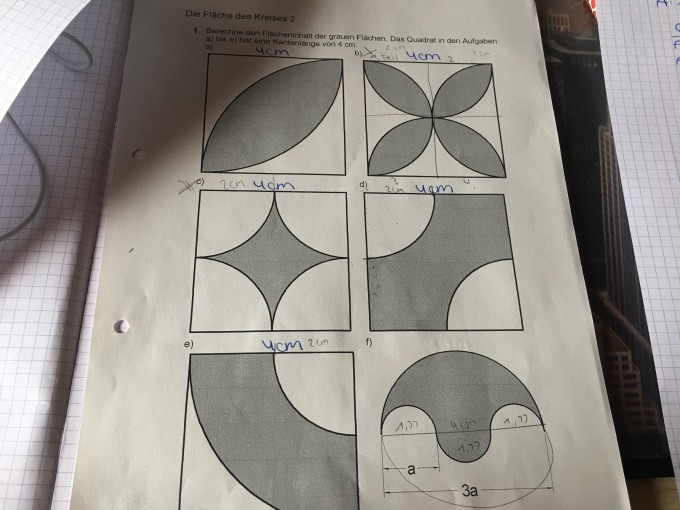
Wollte fragen ob meine Lösungen stimmen:
Kleiner weißer Kreis
\(A= \pi \cdot r^{2}\)
\( = \pi \cdot 1,33 \mathrm{cm}^{2} \)
\( = 4,1783 \,\mathrm{cm}^{2} \)
zusammen
A= \( 25,1325 \,\mathrm{cm}^{2}+2,08915\, \mathrm{cm}^{2}=27,2216 \)
$$ 27,22165\,\mathrm{cm}^{2}-4,1783\, \mathrm{cm}^{2}=23,0433 $$
$$\text{Kreis (weiße)}\\A=π\cdot r^2\\=π\cdot 4 \,cm^2\\ =\frac{50,265\,cm^2}{4}=12,566\,cm^2\\[10pt] \text{Kreis, schwarz}\\ A=π\cdot r^2\\ =π\cdot 2\,cm^2\\ =\frac{12,566\,cm^2}{4}-3,1415\,cm^2\\ =12,566\,cm^2-3,1415\,cm^2\\[20pt] \text{Quadrat}\\ A=a\cdot a\\ =4\,cm\cdot 4\,cm\\=16\,cm^2\\[15pt] zusammen:\\ A=16\,cm^2 - 9,4245\,cm^2 =6,5755\,cm^2 $$
\( großer Kreis \)
\(A =\pi \cdot r^{2} \)
\( A = \pi \cdot 4 \, \mathrm{cm}^{2} \)
\(A=\frac{50,265\, \mathrm{cm}^{2}}{2}=25,1325 \,\mathrm{cm}^{2} \)
kleiner schw.Kreis
\( A=\pi \cdot r^{2} \)
\(=\pi \cdot 1,33 \, \mathrm{cm}^{2} \)
\( =4,1783\, \mathrm{cm}^{2} \)
\( A = 4,1783 \,\mathrm{cm}^{2}:2=2,08915 \,\mathrm{cm}^{2} \)