Ansatz Volumenintegral mit Mantelflächen: EDIT: Fragestellung mit Vektorfeld in Kommentar ca. Nr. 6

Question

ich habe etwas Probleme die folgende Aufgabe zu lösen.

Wäre es korrekt einmal das Volumen mit  0 ≤ r ≤ 1 und einmal mit 1 ≤ r ≤ 4 zu berechnen und diese dann zu addieren?

Comments

Sollst du denn nun das Volumen oder die Mantelfläche ausrechnen? 

Und wovon denn? Warum willst du addieren? Bei einem Volumen müsstest du eher subtrahieren oder direkt nur von r = 1 bis r=2 integrieren.

Ist irgendetwas über z bekannt?

---

Ich dachte das reicht schon für einen Ansatz.

$$Z = {(x,y,z) \in R^3 : 1 < x^{2} + y^{2} < 4 , | z |< 1}$$

mit außerem Normanevektor N an Z.

Warum denn nur von r= 1 bis r=2?

---

Ich stelle mir eine zylindrische Röhre der Länge 2 mit Innenradius 1 und Aussenradius 2 vor und benutze den Pythagoras.

---

ich verstehe leider nicht wie der Außenradius 2 zustande kommt, x² + y² = 4

---

x² + y² = 2²

---

oups.

Was ist der Unterschied zwischen dem Integral über die Mantelflächen und dem Integral über

Angenommen, die Divergenz wäre div(f) = 1

---

Das überlasse ich jetzt gern jemandem, der mehr Übung hat mit Divergenz.

Erkläre vielleicht mal noch in einem Kommentar, was es mit deiner Aufgabe auf sich hat.

---

@ cvda es wäre vielleicht sinnvoll, wenn du mal eine Aufgabe vollständig einstellst und nicht immer irgendeinen Teilfetzen, bei dem erst in den Kommentaren ersichtlich wird, wo das Problem liegt ;)

Es ist bisher immer noch nicht klar was genau berechnet werden soll.

---

Ich entschuldige :P

Seien $$Z = \{(x,y,z) \in R^3 : 1 < x^{2} + y^{2} < 4 , | z |< 1\}$$

Das Vektorfeld ist gegeben durch

$$f(x,y,z) = ( x cos(z)^{2} + x^{2} yz , ysin(z)^{2} + 1, -xyz^{2} + e^{x^{2} + y^{2}} )$$

daraus folgt

$$div(f) = 1$$

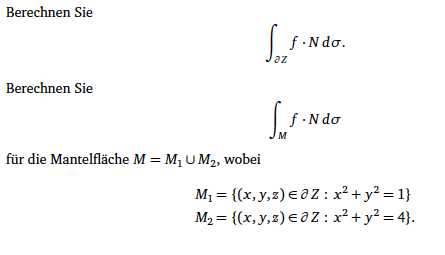
bei dem ersten Integral folgt mit Satz von Gauß 6*π. Wo liegt jetzt der Unterschied zum zweiten Integral mit den beiden Mantelflächen? Wie muss ich die Grenzen ziehen um es unter Verw. von Zylinderkoord. zu berechnen?

---

Der Unterschied zwischen $\partial Z$ und $M$ ist, dass bei $M$ die beiden Kreisringe am Boden und am Deckel der Hohlzylinderoberflaeche $\partial Z$ fehlen. Vielleicht machst Du mal eine Skizze?

---

ich muss eingestehen, ich kann es mir nicht wirklich vorstellen, wie bei einem volumen der deckel fehlen soll :D bzw. wie ich das berechnen soll :/

---

https://www.google.de/search?q=hohlzylinder&tbm=isch

https://de.bettermarks.com/wp-content/uploads/media/kem_FuV3_FuV3Koe…

---

Wenn ich bei dem ersten Integral zwischen 1 < r < 2 wähle, fehlt der mittlere Teil doch auch. So habe ich mir das vorgestellt.

Jedoch kann ich mir das fehlen der Kreisringe nicht vorstellen, bzw. was für Auswirkungen das bei der Berechnung hat.

Edit: Also einmal Volumen von 0< r < 1 und 0 < r < 2 ?

---

Sag mal: Ist dieses Bild nicht deutlich genug?

https://de.bettermarks.com/wp-content/uploads/media/kem_FuV3_FuV3Koe…

Da sind doch jetzt wirklich alle Einzelteile klar zu sehen. M₁ ist die kleine Klopapierrolle und M₂ die grosse. Und die beiden Kreisringe sind Boden und Deckel. Und alles zusammen ist das Gebilde ganz links: ∂Z.

Und die Aufgabe verlangt von Dir, einmal ein Oberflaechenintegral ueber M₁ ∪ M₂ und einmal eines ueber ∂Z auszurechnen. Von Volumen lese ich nichts.