Kirchturm am Hang. Problem bei d.

Question

Geometrie: Komplexe Aufgaben - Kirchturm am Hang

Eine Bergwiese bildet einen ebenen, Ieicht geneigten Kirchturm. Auf dem Hang steht ein alter Kirchturm, das Dach des Turms hat die Form einer quadratischen Pyramide mit der Höhe 10. Für die Punktkoordinaten in der Abbildung gilt:

A(10|0|0), B(10|10|0), C(0|10|2), E(10|0|20).

a) Bestimmen Sie eine Parametergleichung der Hangebene ε.

b) Zeigen Sie, dass der Vektor $\vec{v}$ senkrecht zur Hangebene $\varepsilon$ steht.

c) Wie groß ist der Abstand der Pyramidenspitze S zur Hangebene ε?

d) Zu einer bestimmten Tageszeit fällt das Sonnenlicht in Richtung des Vektors $\vec{u}$ ein. Die Dachfläche mit den Solarzellen wird nun exakt senkrecht getroffen. Um welche der vier Dachflächen handelt es sich? An welcher Stelle $S^{\prime \prime}$ des Hangs liegt nun der Schattenpunkt der Turmspitze S? Ein Punkt P im Innern des Dachraums ist von allen fünf Ecken der Dachpyramide exakt gleich weit entfernt. Bestimmen Sie die Höhenkoordinate p des Punktes.

Answer 1

a) hast Du schon gelöst. Die Parameterform der Ebene $e$ (Hang) könnte z.B. heißen

$$e(r,s) = D + r\cdot DA + s \cdot e_y$$ das macht: $$e(r,s) = \begin{pmatrix} 0\\0 \\ 2\end{pmatrix} + r \begin{pmatrix}10 \\ 0\\ -2\end{pmatrix} + s\begin{pmatrix} 0\\ 1\\ 0\end{pmatrix}$$

Die Geradengleichung des Lichtstrahls $h(t)$ ist z.B.:

$$h(t) = S + t \cdot u= \begin{pmatrix} 5\\ 5\\ 30\end{pmatrix} + t \begin{pmatrix} 0\\ -2\\ -1\end{pmatrix}$$

Den Schnittpunkt des Lichtstrahls $h$ mit der Hangebene $e$ erhält man, wenn man beide gleich setzt $e(r,s)=h(t)$ und eine Lösung für die Parameter $r$, $s$ und $t$ sucht - also:

$$\begin{pmatrix} 0\\0 \\ 2\end{pmatrix} + r \begin{pmatrix}10 \\ 0\\ -2\end{pmatrix} + s\begin{pmatrix} 0\\ 1\\ 0\end{pmatrix}= \begin{pmatrix} 5\\ 5\\ 30\end{pmatrix} + t \begin{pmatrix} 0\\ -2\\ -1\end{pmatrix}$$

Umordnen ergibt$$r \begin{pmatrix}10 \\ 0\\ -2\end{pmatrix} + s\begin{pmatrix} 0\\ 1\\ 0\end{pmatrix}+ t \begin{pmatrix} 0\\ 2\\ 1\end{pmatrix}= \begin{pmatrix} 5\\ 5\\ 28\end{pmatrix}$$ oder anders geschrieben:

$$\begin{pmatrix}10 & 0 & 0 \\ 0 & 1& 2\\ -2 & 0& 1\end{pmatrix} \cdot \begin{pmatrix} r\\ s\\ t\end{pmatrix}= \begin{pmatrix} 5\\ 5\\ 28\end{pmatrix}$$ In diesem Fall reicht es aus, die oberste Gleichung $10 r=5$ durch 5 zu dividieren und das Ergebnis $2r=1$ zur untersten Gleichung $-2r + t = 28$ zu addieren:

$$0r + t = 28+1 \quad \Rightarrow t=29$$ Nach Einsetzen in $h(t)$ erhält man:

$$S'' = \begin{pmatrix} 5\\ 5\\ 30\end{pmatrix} + 29 \begin{pmatrix} 0\\ -2\\ -1\end{pmatrix}= \begin{pmatrix} 5\\ -53\\ 1\end{pmatrix}$$

Ich habe Dir das ganze noch mal im Geoknecht3D eingegeben:

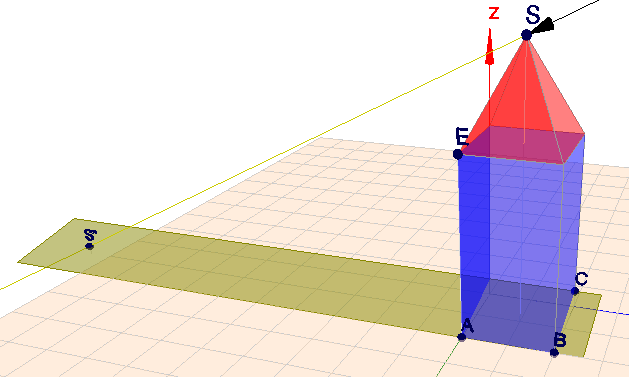
(klick auf das Bild)

Gruß Werner

Answer 2

Nun,

nach dem u_x = 0 ist muss eine Dachkante parallel zur x-Achse sein und mit u_y = -2 muss es die Kante FG sein. - Du kannst den Vektor einfach ins KO rein malen oder die Skalarprodukte (?=0) ausrechnen.

Lege eine Gerade h(t):=S+t u und schneide die Gerade mit der Hangebene.

Dazu nehmen wir am besten die Koordinatenform der Ebene und setzen die Gerade ein:

(v (h(t) - B)) = 0 -> t=29 ->h(29) -> S''=(5, -53, 1)

Comments

Tut mir leid aber ich hab das leider nicht verstanden.

---

Was hast Du nicht verstanden?

---

Was ist u_x? Was ist KO? Wie lautet die gerade h(t)?

---

u_x = x Koordinate von u (wie viele 0en kommen in u vor?)

KO Koordinatensystem

Eine Gerade wird üblicherweise durch einen Punkt (S) und eine Richtung (u) beschrieben, die Verlängerung/Verkürzung der Richtung erfolgt durch einen Laufparameter t oder gerne auch Lamda genannt - wie belieben.

Alle Angaben entsprechend der Aufgabe

---

Danke.

Ich versteh den Teil ab dem die gerade h(t) die gerade mit der hängenden schneidet leider nicht könnten Sie mir das nochmal erklären Danke.

---

Die allgemein Koordinatengleichung einer Ebene;

$$n {\left( \left( \begin{array}{r}x\\y\\ z\\ \end{array} \right) - O \right) =0 }$$ 

Bei Deiner Aufgabe ist der Normalenvektor n = v und der Ebenenpunkt O = B. Zur Schnittpunktberechnung setzt Du die Gerade (x,y,z) = h(t)  ein und berechnest t, das eingesetzt in h(t) dann den Schnittpunkt ergibt - alles klar?