Hallo B.k
du hast für die gesuchte Funktion f folgende Bedingungen:
Der Graph ist zur y Achse symmetrisch
→ im Funktionsterm dürfen bei x nur gerade Exponenten vorkommen
Zusätzlich
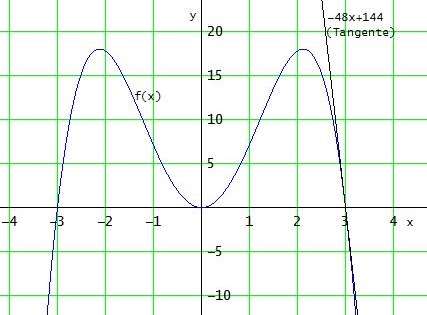
bei a): f(0) = 0 ; f(3) = 0 ; f '(3) = -48 (die Klammeraufgaben lasse ich weg)
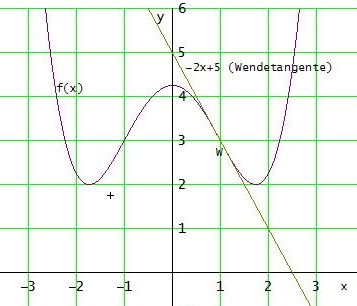
bei b): f(1) = 3 ; f "(1) = 0 ; f '(1) = -2
Mit diesen jeweils 3 Bedingungen kannst du jeweils 3 Unbekannte bestimmen.
Der einfachste Ansatz für die Funktionsgleichung ist daher f(x) = ax4 + bx2 + c
Ableitungen: f '(x) = 4ax3 + 2bx ; f "(x) = 12ax2 + 2b
Bei a) ergibt sich:
f(0) = a·04 + b·02 + c = 0 → c = 0
f(3) = 81a + 9b = 0 → b = - 9a
f '(3) = 108a + 6b = - 48 → 108a - 54a = - 48 → 54a = -48 → a = - 8/9
→ b = 8
f(x) = - 8/9 · x4 + 8 · x2
Bei b) ergibt sich:
f(1) = a + b + c = 3
f "(1) = 12a + 2b = 0
f '(1) = 4a + 2b = - 2
G2 - G3 → 8a = 2 → a = 1/4
a in G3 → b = -3/2 ; a,b in G1 → c = 17/4
f(x) = 1/4 · x4 - 3/2 · x + 17/4
Wolfgang