Lücke, Pol, Nullstelle gebrochen rationaler Funktion, Zähler 3. Binom

Question

Hallo :)

Könnte mir eventuell jemand bei dieser Aufgabe behilflich sein? Bin etwas überfragt...


Dabei sollen wir herausfinden, ob sie an diesen Stellen eine Nullstelle, Polstelle, Hebbare Lücke  oder weder Defintionslücke noch Nullstelle besitzt:
x = 1
x = 0
x = -2
x = 2
x = 4

Answer 1

Nullstellen : Zähler = 0
x^2 - 4 = 0
x = -2
und
x = 2
( -2 | 0 ) ( 2 | 0 )

Division durch 0 bei
( x -1 ) * x = 0
Satz vom Nullprodukt anwenden
x = 0
und
x = 1
sind Polstellen

Hebbare Lücken gibt es keine

Comments

Dankeschön :) Also wäre dann x = 4 auch eine Nullstelle ?

---

Nein. Der Punkt P(4|0) liegt nicht auf dem Graphen. Grund: 4^2 - 4 = 12 ≠ 0 .

Answer 2

Hallo Lucy,

f(x) =  [ (x-2) * (x+2) ] / [ x * (x-1) ]         D = ℝ \ { 0 ; 1 }  

Der Nenner hat die Linearfaktoren x  und x-1. Deren Nullstellen x=0 und x=1  sind die Definitionslücken.

Eine Definitionslücke ist

-  eine Polstelle, wenn man den zugehörigen Linearfaktor nicht wegkürzen kann, was hier in beiden Fällen der Fall ist.

-  eine hebbare Lücke, wenn man den zugehörigen Linearfaktor wegkürzen kann (hier nicht der Fall)

Die Nullstellen  x=2 und x=-2  des Zählers sind beide Nullstellen von f, weil sie im Definitionsbereich der Funktion liegen.

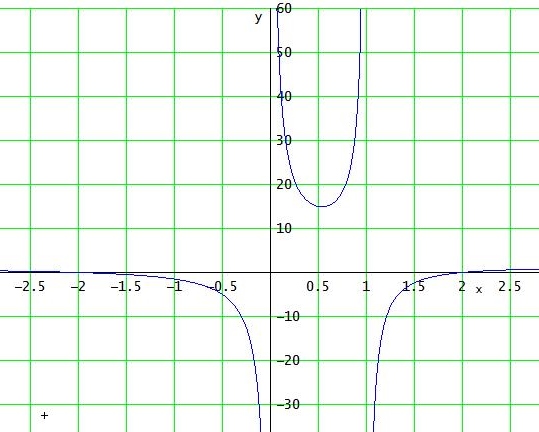
Im Graph kann man die Polstellen daran erkennen, dass die Funktionswerte bei Annäherung von x an diese Stellen gegen "± unendlich" streben.

Gruß Wolfgang

Comments

Dankeschön :) Also wäre dann x = 4 auch eine Nullstelle ?

---

> Also wäre dann x = 4 auch eine Nullstelle ?

Nein, denn    f(4)  =  (4² - 4) / ( 4 * 3) = 12/12 = 1  ≠ 0

Nullstellen von f  sind nur die Nullstellen x = ± 2 des Zählers.