Umkehrung des Zweispiegelungssatzes?

Question

Gegeben sei ein Quadrat ABCD [Zeichnen Sie dazu ein Quadrat der Seitenlänge 4 cm]. Wir nennen AB = a, BC = b, CD = c, DA = d und AC = e. Die Gerade durch die Mittelpunkte der Strecken a und c sei mit f sowie der Mittelpunkt des Quadrats mit M bezeichnet.

1. Nennen Sie zwei verschiedene Doppelspiegelungen, die mit der Drehung dC,90◦ übereinstimmen.
2. Nennen Sie eine weitere Doppelspiegelung, die die Abbildung sf ◦ se beschreibt. Verwenden Sie dabei die Achse e.
3. Nennen Sie eine weitere Doppelspiegelung, die die Abbildung sb ◦ sf beschreibt. Verwenden Sie dabei die Achse f.
4. Beantworten Sie folgende Frage: Warum sind bei Doppelspiegelungen senkrecht aufeinander stehende Achsen von Vorteil? 

Answer 1

Hallo Luisa,

Jede Doppelspiegelung an zwei Achsen entspricht einer Drehung um den Schnittpunkt der Achsen um den doppelten Winkel, den die Achsen zueinander haben. Mit diesem Wissen im Hintergrund sollte sich die Aufgabe lösen lassen.

1.) Ich unterstelle, dass mit $\text{d}C \space 90°$ eine Drehung um $90°$ des Quadrats um den Punkt $C$ gemeint ist. Damit benötigt man für die Doppelspiegelung zwei Achsen, die durch $C$ laufen und im Winkel von $45°$ zueinander stehen.

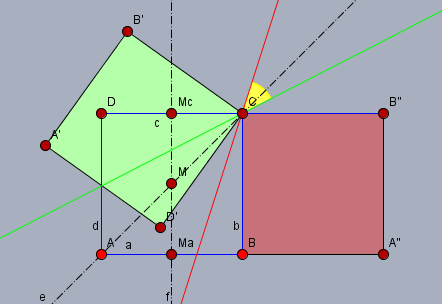
Es spielt dabei keine Rolle wie die Achsen liegen. Ich habe Dir das oben mal eingezeichnet. Erst wird um die grüne Achse  gespiegelt, es entsteht das grüne Quadrat und anschließend um die rote zum roten Quadrat. Beide stehen im Winkel von $45°$ (gelb) zu einander. Damit kann man statt der grünen und rote Achse auch die Seiten $c$ und die Gerade $e$ oder die Gerade $e$ und die Seite $b$ wählen:

$$\text{d}C \space 90° = \text{s}c \circ \text{s}e$$

$$\text{d}C \space 90° = \text{s}e \circ \text{s}b$$

2.) ist dann nach den obigen Überlegungen:

$$\text{s}f \circ \text{s}e = \text{s}f \circ \text{s}g = \text{d} M \space 90°$$

$g$ ist eine Gerade durch $M$ und parallel zu $a$. Entscheidend ist, dass $g$ auch im Winkel von $\angle (f,e) = 45°$ zu $e$ steht.

3.) $b$ und $f$ stehen parallel. Streng genommen ändert sich nichts an dem oben gesagten, nur dass der Schnittpunkt jetzt im Unendlichen liegt und aus der Drehung damit eine Verschiebung um den doppelten Abstand der Spiegelachsen wird. Und es spielt wieder keine Rolle wo diese Spiegelachsen liegen. Also ist z.B.:

$$\text{s}b \circ \text{s}f =\text{s}f \circ \text{s}d$$

 

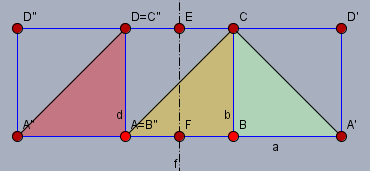
4.) Wenn der Winkel der Spiegelachsen $90°$ beträgt, so beträgt der dazu gehörige Rotationswinkel $2 \cdot 90°=180°$. Und somit ist die Abbildung auch eine Punktspiegelung, die sich leicht konstruieren lässt.

Gruß Werner

Comments

Wow, ich bedanke mich.Hätte niemals mit so einer ausführlichen Antwort gerechnet. DANKE!

---

Bitteschön - gern geschehen! Es freut mich, wenn Dir meine Antwort weiter hilft.