Anwendungsbeispiel der Umkehrung des Satz des Thales

Question

Liebe Lounge,

ich bin auf der Suche nach einer Konstruktionsaufgabe, bei welcher die UMKEHRUNG des Satz des Thales benötigt wird.

Satz des Thales: Punkt C eines Dreiecks ABC liegt auf dem Thaleskreis → y=90°

Umkehrung: Dreieck ABC hat 90° Winkel bei y → C liegt auf Thaleskreis mit Durchmesser AB.

Vielen Dank!

Comments

z.B. gelingt die Konstruktion einer Tangente an den Kreis durch einen Punkt außerhalb des Kreises ebenfalls durch Anwendung des Satzes NICHT durch Anwendung seiner Umkehrung...

---

Wäre vielleicht eine Anwendung, dass man mit Hilfe der Umkehrung den Mittelpunkt eines vorgegebenen Kreises bestimmen kann?

Man kann dann nämlich einen beliebigen Punkt C auf der Kreislinie markieren. Von dort aus die beiden Katheten mit einem rechten Winkel einzeichnen. Die beiden Schnittpunkte A und B der Katheten mit der Kreislinie verbinden.

Die entstandene Strecke ist laut Umkehrung des Satz des Thales der Durchmesser des Kreises. Wenn ich nun die Mittelsenkrechte konstruiere habe ich den Mittelpunkt des Kreises gefunden.

Was haltet ihr von dieser Idee?

Answer 1

Konstruktionsaufgabe, bei welcher die UMKEHRUNG des Satz des Thales benötigt wird:

Zeige, das das Dreieck ABC mit A(-1|0), B(1|0) und C(√3/2|1/2) rechtwinklig ist.

Comments

Aber bei der Umkehrung wird ja gerade vorausgesetzt, dass es rechtwinklig ist?

---

Irrtum meinerseits.

Answer 2

Hallo,

1. Möglichkeit

stelle eine Leiter der Länge \(l\) an eine senkrechte Wand. Wenn die Leiter nun über den horizontalen Boden und an der senkrechte Wand hinunter rutscht, welcher Art ist dann die (Orts-)Kurve, die der Mittelpunkt \(M\) der Leiter beschreibt?

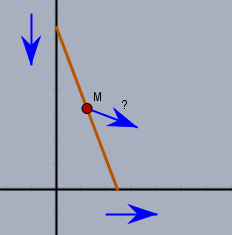
Bzw.: konstruiere den Weg von \(M\).

2. Möglichkeit

Keine Konstruktion, aber ein Beweis:

Beweise, dass der Schnittpunkt \(S\) einer inneren und einer äußeren jeweils gemeinsamen Tangenten zweier Kreise, deren Mittelpunkte \(M_1\) und \(M_2\) sind, auf dem Thaleskreis durch \(M_1M_2\) liegt.

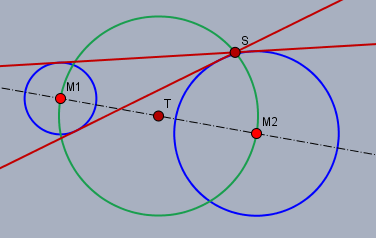
Für einen Beweis braucht man die Umkehrung des Satzes von Thales.

Comments

... kannst du mir helfen?

---

... kannst du mir helfen?

bei welchem Problem genau? bei der Kommentierung Deines Kommentars ..

... Was haltet ihr von dieser Idee?

oder bei der Lösung, der von mir gestellten Aufgabe?

---

1. Meine Idee mit der Bestimmung des Mittelpunktes (hier wird doch die Umkehrung benutzt - oder?

2. Wird bei der Aufgabe von Roland tatsächlich die Umkehrung benutzt oder doch wieder nur der eigentliche Satz? -> Dazu tendiere ich nämlich)

3. Zu guter letzt gerne eine Hilfe zu deiner Aufgabe :)!

---

Beziehungsweise wäre folgende Aufgabe auch über die Umkehrung möglich:

Zeichne zu einem gegebenen rechtwinkligen Dreieck den Umkreis.

---

Könntest du den Beweis mal skizzieren bitte? Und ganz deutlich machen, wo du die Umkehrung des Satzes benutzt?

---

1. Meine Idee mit der Bestimmung des Mittelpunktes (hier wird doch die Umkehrung benutzt - oder?

Ja - die Umkehrung des Satzes besagt, dass der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks im Mittelpunkt der Hypotenuse liegt.

2. Wird bei der Aufgabe von Roland tatsächlich die Umkehrung benutzt oder doch wieder nur der eigentliche Satz? -> Dazu tendiere ich nämlich)

Ja - da hast Du wohl recht.

3. Zu guter letzt gerne eine Hilfe zu deiner Aufgabe :)!

Interessant, dass Du das nicht sofort siehst. ;-)

Das rechtwinklige Dreieck ist doch nicht zu übersehen. Zeichne doch mal einen Kreis mit Durchmesser \(l\) um \(M\). Und das auch noch für verschieden Positionen der Leiter:

Nach der Umkehrung des Satzes von Thales geht der Kreis mit Durchmesser \(l\) immer durch \(O\). Die Strecke \(|OM|\) ist also konstant unabhängig von der Lage der Leiter. \(l\) und damit der Radius des Kreises bleibt doch immer konstant.

PS.: ich habe übrigens meine Antwort noch um eine weitere Möglichkeit erweitert.

---

Nach der Umkehrung des Satzes von Thales geht der Kreis mit Durchmesser
l
immer durch
O
. Die Strecke ||
|
O
M
|
ist also konstant unabhängig von der Lage der Leiter.
l
und damit der Radius des Kreises bleibt doch immer konstant.

Okay, das leuchtet mir ein.

Also liegen liegen alle Mittelpunkte auf einem neuen Kreis, welcher als Mittelpunkt den Punkt O besitzt und den Radius l/2 hat.

---

Die Herangehensweise für den Beweis deiner 2. Möglichkeit sehe ich allerdings noch nicht ... :(

---

Also liegen liegen alle Mittelpunkte auf einem neuen Kreis, welcher als Mittelpunkt den Punkt O besitzt und den Radius l/2 hat.

So ist das :-)

Die Herangehensweise für den Beweis deiner 2. Möglichkeit sehe ich allerdings noch nicht ..

Für die Umkehrung des Satzes von Thales muss irgendwo ein rechter Winkel auftauchen - oder! Den rechten Winkel findet man, wenn man beide Winkelhalbierenden durch \(S\) bezogen auf die beiden Tangenten einzeichnet (blau):

die Winkelhalbierenden stehen immer senkrecht auf einander und verlaufen zwangsläufig durch die Mittelpunkte \(M_1\) und \(M_2\) der Kreise. Also ist das Dreieck \(\triangle M_1M_2S\) rechtwinklig und daraus folgt, dass der Thaleskreis über \(M_1M_2\) auch durch \(S\) geht.

---

Für einen Beweis braucht man die Umkehrung des Satzes von Thales.

Mit dem "Brauchen" ist das so eine Sache.

Man könnte den Sachverhalt natürlich auch beweisen ohne die Umkehrung zu zitieren (und sich dann hinterher darüber freuen, dass man womöglich eben diese Umkehrung sozusagen en passant mit bewiesen hat).

Ohne diese Umkehrung lässt sich auch das Leiter-Problem leicht durch Anwenden des Pythagoras lösen : Wenn die Leiter der Länge l die Koordinatenachsen bei a und b schneidet, so hat ihr Mittelpunkt die Koordinaten (a/2 | b/2) und sein Abstand zum Koordinatenursprung ist die Wurzel aus (a/2)² + (b/2)² = wurzel aus (a² + b²)/4 = l/2 konstant.

Noch so eine Aufgabe : Bestimme die Ortskurve der Mittelpunkte aller Sehnen eines Kreises, die durch einen festen Punkt P auf der Kreislinie verlaufen.

---

Mit dem "Brauchen" ist das so eine Sache.

.. ich wußte, dass Du kommst, als ich diesen Satz hingeschrieben hatte ;-). Interpretiere das 'einen' in ...

Für einen Beweis braucht man die Umkehrung des Satzes von Thales.

... doch als 'irgend einen'. So war es jedenfalls gemeint. Ich bin sicher nicht so naiv zu glauben, dass es für irgend einen Satz der Mathematik nur genau einen einzige Art von Beweis gibt ;-)

---

Noch so eine Aufgabe : Bestimme die Ortskurve der Mittelpunkte aller Sehnen eines Kreises, die durch einen festen Punkt P auf der Kreislinie verlaufen.

auch schön!