Kartesische Form in Polarform anhand -3.941 + 1.690 · i

Question

Wie kann man komplexe Zahlen von kartesischer Form in Polarform umwandeln.

Könntet Ihr mir das bitte anhand dieser komplexen Zahlen erklären:

1. $-3.941 + 1.690 · i$

2. $z_3= 1+y_3·j$ berechnen → $y_3 = 0.7$

Das heißt $z_3= 1+0.7 · j$ muss auch in Polarform umgewandelt werden.

3. $z_ = (z_3)^5$ in kartesische und Polarform.

Answer 1

Aufgabe 1:

$$\begin{array}{l}{z=-3,941+i1,69} \\ {\left|z_{1}\right|=\sqrt{(-3,941)^{2}+(1,69)^{2}}} \\ {\left|z_{1}\right| \approx 4,288} \\ {\tan \varphi=\frac{1,69}{-3,941}=-0,4288} \\ φ\quad{\approx 156,80} \\ {\Rightarrow z=4,288 \cdot e^{i 156,80^{\circ}}} \\ {z=4,288 \cos \left(156,8^{\circ}\right)+i \sin \left(156,8^{\circ}\right)}\end{array}$$

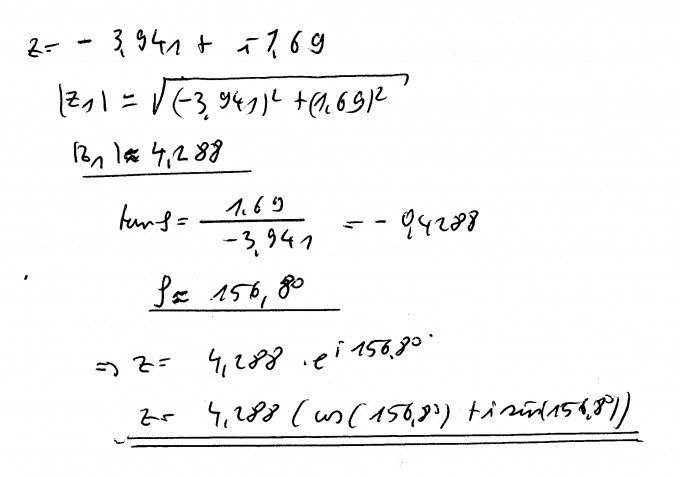
Wurde phi mit arctan und das Ergebnis + 180 berechnet?

Ja, weil 2. Quadrant.

Aufgabe 2 und 3:

z₃= 1.22 e ^{i 35°}

z₄= 2.7  e^{i 175°}

$$\begin{array}{l}{z_{3}=1+i0,7} \\ {|z|=\sqrt{1^{2}+0,7^{2}}} \\ {|z| \approx 1.22} \\ {\tan \varphi=\frac{0,7}{1}=0,7(1 .\text { Quadrant) } } \\ {\varphi \approx 35^{\circ}} \\ {\Rightarrow z_{3}=1,22 \mathrm{e}^{i35^{\circ}}} \\ {z_{3}=1,22\left(\cos \left(35^{\circ}\right)+i \sin \left(35^{\circ}\right)\right)}\end{array}$$

$$\begin{aligned} z_{4} &=\left[1,22 \cdot e^{i 35^{\circ}}\right]^{5} \\ &=1,22^{5} \cdot e^{i 175^{\circ}} \\ \Rightarrow & z_{4}={2,7} \cdot e^{i 175^{\circ}} \\ &=2,7\left(\cos \left(175^{\circ}\right)+i \sin \left(175^{\circ}\right)\right) \end{aligned}$$

Comments

Wie kommt man von 1.22*e^175°·i auf 2.7*e^175°·i?

---

Es gibt da ein Potenzgesetz:

(a b)^m=a^m *b^m