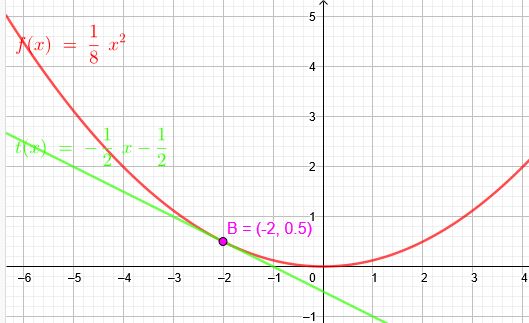
\(f(x)=\frac{1}{8} x^2\) Bestimme Tangente und Berührpunkt B der Geraden \(g: y=-\frac{1}{2} x+n\)
\(\frac{1}{8} x^2=-\frac{1}{2} x+n\)
\(\frac{1}{8} x^2+\frac{1}{2} x=n\)
\( x^2+4x=8n\)
\( (x+\red {2})^2=8n+4\)
Die Berührstelle ist bei \(x=-\red {2}\) \(f(-2)=\frac{1}{2} \)
Berührpunkt B\((-2|\frac{1}{2})\)
B\((-2|\frac{1}{2})\) liegt auf \(g \)
\( \frac{1}{2}=-\frac{1}{2}\cdot (-2)+n\)
\( n=-\frac{1}{2}\)
Tangente \(t(x)=-\frac{1}{2} x-\frac{1}{2}\)