Partialbruchzerlegung von (1+ z^7)/(z^5 + z^3) im Komplexen,

Question

Hi, könnte mir Jemand sagen, ob dies bisher so stimmt und wie es nun weiter geht?

Partialbruchzerlegung von (1+ z^7)/(z^5 + z^3)  im Komplexen,

Comments

Tipp: Matheartikel von Unknown https://www.matheretter.de/wiki/partialbruchzerlegung#nstkmpl falls noch nötig. 

Answer 1

Meine Berechnung:

Comments

Zwei Fragen.

1. Warum Dx?

2. Kann es sein, dass wir beide etwas falsch machen? Denn es geht hier ja um eine komplexe Zerlegung. Also müsste man ja (z+i)(z-i) irgendwo unterbringen oder?

---

Vlt so in der Art?

---

Also müsste man ja (z+i)(z-i) irgendwo unterbringen oder?

Statt (Dz + E)/(z^2 + 1) kannst du

F/(z-j) + G/(z+j) schreiben. 

EDIT: Hast du ja gerade getan :) 

---

:) Nur komme ich auf keine Lösung beim Koeffizientenvergleich. Ich stelle es in 3 Minuten mal hier rein.

Ist es eigentlich ok hier solche Bilder zu Posten? Oder sollte man es lieber in Latex eintippen?

---

Das ist bei dir alles gut lesbar. Du solltest aber die Fragestellung abtippen. Ich habe wenigstens mal eine Formel in die Überschrift genommen. Ähnliche Fragen werden v.a. via Überschrift und Tags (sowie Text der Frage) gesucht. 

---

Ok, werde ich beim nächsten Mal beachten.

Also hier mal meine Rechnung, wobei ein Widerspruch entsteht

Answer 2

Nimm vielleicht https://www.wolframalpha.com/input/?i=(1%2B+z%5E7)%2F(z%5E5+%2B+z%5E3)

Hier musst du nur noch eine PBZ von (z+1)/(z^2 +1) rechnen. 

EDIT: Antwort von Fragesteller selbst ist weiter unten zu finden. 

Comments

Mmh, auch hier komme ich auf nichts richtiges: Jedenfalls nicht nach Wolfram, also irgendwas mache ich falsch, denn es muss ja auch wie unten funktionieren. Es ist eine Klausuraufgabe mit 2Punkten

---

Vielleicht so:

b = (1+i)/(2i)  | Erweitern mit -i

b = (-i(1+i))/(2*1) 

= (-i + 1)/2 

= 1/2 - 1/2 i.  

a analog. 

---

Job, dass ist es danke.

Jetzt muss ich nur noch herausfinden, warum es dort unten scheitert.

---

Kurze Frage, mit analog meinst du die Erweiterung mit i, statt -i, oder?

---

Ich würde auch mit (-i) erweitern. Aber es ist eigentlich egal, ob ein Minus unter / über oder vor einem Bruchstrich steht. 

---

Oh ok, na wenn das egal ist, dann ist ja gut:)

Eine Frage habe ich aber noch.

Was mache ich mit dem Wert aus der Polynomdivision, schreibt man dort einfach (x-1) dazu?

---

Wo meinst du genau? Aus der Polynomdivision hast du doch schon z^2 - 1 +  Bruch. 

Nur beim Bruch musst du noch die Partialbruchzerlegung machen. Du darfst statt Bruch auch Bruch1 + Bruch2 separat zerlegen. 

---

Also es geht um die (x^2-1). Wie gebe ich die zum Schluss an?

Denn ich soll ja den ganzen Ausdruck zerlegen und da gehört nun einmal die (x^2-1) dazu. Also wie gebe ich das mathematisch korrekt an, kann es ja nicht einfach da oben stehen lassen:)

Und ich habe noch eine Frage zu dem Bild hier:

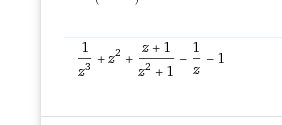
Dies stellt ja die Zerlegung in R dar.

Aber wo kommt die -1 bzw. das z^2 her?

Nach meiner nun eigentlich korrekten Rechnung, müsste es 0/z^2 lauten und das fällt ja weg und bei der -1 habe ich keine Ahnung, wo man die herholt 

---

Hat sich erledigt, manchmal sieht man den Wald vor Lauter Bäumen nicht mehr.

Ich bedanke mich für die Hilfe.

---

Bitte. Gern geschehen!