Vorwort:
Der Satz des Heron, im Englischen "Heron's formula" ist nach dem Mathematiker Heron von Alexandria benannt. Er ist außerdem bekannt für das "Heron-Verfahren" zum Berechnen von Quadratwurzeln bekannt. Herons Werke sind teilweise nur fragmentarisch überliefert; meist nur bestehend aus einigen Fetzen Vorlesungsnotizen. Den Satz des Heron auf der anderen Seite hat er in seinem Buch "Metrica", welches 60 n. Chr. geschrieben wurde, notiert und bewiesen.

Satz des Heron:
Dieser Artikel wird einzig und allein vom Satz des Heron handeln, welcher verwendet wird, um den Flächeninhalt eines Dreiecks mit drei gegebenen Seiten zu berechnen. Hierbei ist es völlig egal, welcher Art von Dreieck ihr begegnet. Der Satz des Heron wird euch immer treu bleiben. Er ist also universell anwendbar.
Der Satz des Heron besagt Folgendes:$$ F_{\Delta}=\sqrt[]{s(s-a)(s-b)(s-c)} $$ Wobei der Parameter "s" wie folgt bestimmt wird:$$ s=\frac{a+b+c}{2} $$ Das ist die normale Darstellung des Satzes. Es gibt jedoch andere Darstellungen, deren Ziel es ist, die Formel einfacher und handlicher zu machen. Hier meine Lieblingsdarstellung des Satzes:$$ F_{\Delta}=\frac{\sqrt[]{4a^2b^2-(a^2+b^2-c^2)^2}}{4}$$ Es ist jedoch möglich, dass Heron nicht der Erste war, der zu dieser Erkenntnis kam. Es wird vermutet, dass Archimedes die Formel schon zwei Jahrhunderte vor Heron entdeckte.
Beweisführung über den Satz des Pythagoras:
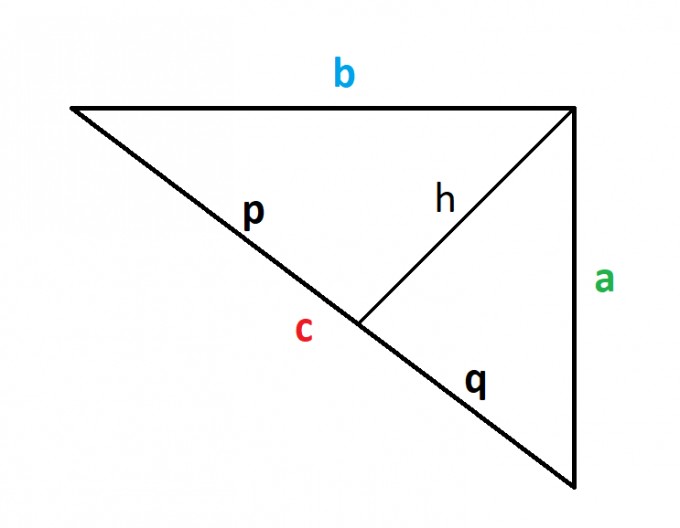
Nach dem Satz des Pythagoras gilt, dass \( \text{b²=h²+p²} \) und \( \text{a²=h²+(c-p)²} \) ist. Subtrahieren wir diese Gleichungen voneinander erhalten wir:$$ a^2-b^2=c^2-2cp $$ Diese Gleichung erlaubt es uns, \(p\) in Bezug auf die Seiten des Dreiecks auszudrücken:$$ p=\frac{-a^2+b^2+c^2}{2c} $$Für die Höhe des Dreiecks haben wir \(h^2=b^2-p^2\). Durch das Ersetzen von "p" durch die oben angegebene Formel und die Anwendung der Differenz der Quadrate Identität erhalten wir:$$ h^2=b^2-\left(\frac{-a^2+b^2+c^2}{2c}\right)^2 $$ Diese müssen wir nun etwas umformen:$$ =\frac{(2bc-a^2+b^2+c^2)(2bc+a^2-b^2-c^2)}{4c^2} $$$$ =\frac{((b+c)^2-a^2)(a^2-(b-c)^2)}{4c^2}$$$$ =\frac{(b+c-a)(b+c+a)(a+b-c)(a-b+c)}{4c^2}$$ Nun müssen wir uns an folgende Gleichung erinnern:$$ s=\frac{a+b+c}{2} $$ Denn jetzt wird das durch die alten Parameter ersetzt:$$ =\frac{2(s-a)\cdot2s \cdot 2(s-c)\cdot2(s-b)}{4c^2}$$$$ =\frac{4s(s-a)(s-b)(s-c)}{c^2}$$Dieses Ergebnis wenden wir nun auf die Formel an, die die Fläche eines Dreiecks aus seiner Höhe berechnet:$$ A=\frac{c \cdot h}{2} $$$$ =\sqrt[]{\frac{c^2}{4}\cdot\frac{4s(s-a)(s-b)(s-c)}{c^2}}$$$$ =\sqrt[]{s(s-a)(s-b)(s-c)} $$ Damit ist mathematisch die Gültigkeit des Satzes des Heron bewiesen. Kommen wir nun also zur Anwendung des Satzes.
Anwendungsbeispiel:
Gegeben ist ein Dreieck, welches gleichschenklig ist. Es werden folgende Angaben gemacht:$$ a=12 \quad c=3cm$$ Hierbei ist nicht zu vergessen, dass bei einem gleichschenkligen Dreieck die beiden Schenkel (a=b) gleich lang sind. Setzen wir die Werte also in den Satz des Herons ein:$$ F_{\Delta}=\frac{\sqrt[]{4\cdot12^2\cdot 12^2-(12^2+12^2-3^2)^2}}{4}=\frac{27\sqrt[]{7}}{4}\approx17.86cm^2 $$
Ich hoffe, dass euch mein Artikel gefällt und das der Satz des Heron mehr Beachtung erhält, da er universell anwendbar und bei vielen Sachverhalten sehr hilfreich ist.