Hallo Peter,
ich verstehe das so, dass der Würfel sich innerhalb des Kegels befindet und seine 4 oberen Ecken die Mantelfläche des Kegels berühren. Also so:
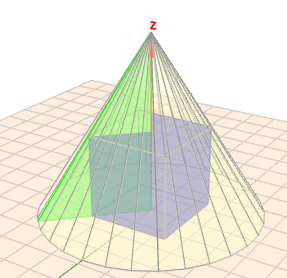
(klick auf das Bild)
Die Würfelseite ist mit \(a\) festgelegt und das Volumen des Kegels soll minimiert werden. Das Volumen \(V\) hast Du richtig beschrieben mit
$$V = \frac13 \pi r^2 h$$
Betrachte nun das grün schattierte Dreieck in der Skizze. Die Grundseite des Dreiecks ist dier Radius des Kegels \(r\) und die Höhe des Dreiecks ist identisch mit der Höhe des Kegels \(h\). Die parallel zur Grundfläche verlaufende Strecke, die die Deckfläche des Würfels mit dem Dreieck bildet ist \(d/2\) , wenn \(d\) die Länge der Diagonale einer Würfelseite ist. Nach dem 2.Strahlensatz ist dann
$$\frac{\frac{d}{2}}{r} = \frac{h - a}{h} \quad \Rightarrow \frac12 dh = r(h-a)$$
das nach \(h\) auflösen gibt
$$h= \frac{ar}{r - \frac{d}{2}}$$
Setzt man die in die Volumengleichung ein und leitet nach \(r\) ab, so bekommt man das \(r\), für das das Volumen maximal wird. Etwas einfacher ist es, nach Lagrange vorzugehen:
$$V(r,h,\lambda) = \frac13 \pi r^2 h + \lambda(r(h-a) - \frac12 dh)$$ $$\frac{\text{d}V}{\text{d}r} = \frac23 \pi rh + \lambda h = 0 \quad \Rightarrow \lambda = -\frac23 \pi r$$ $$\frac{\text{d}V}{\text{d}h} = \frac13 \pi r^2 + \lambda (r-\frac{d}{2}) = 0$$
Einsetzen von \(\lambda\) aus der \(\text{d}V/\text{d}r\) gibt $$\frac13 \pi r^2 -\frac23 \pi r (r-\frac{d}{2}) = 0 \quad \left| \div \frac13 \pi r\right.$$ $$r -2 (r-\frac{d}{2}) = 0 \quad \left| + r\right.$$ $$d = r \quad \text{bzw.: } r = d = a\sqrt{2} \quad \Rightarrow h = 2a$$