Funktionsgleichungen bestimmen. Erlöse gemäß der Funktion E mit E(x)=-0,5x^2+3,5x, wobei x den Absatz in ME angibt.

Question

Ein Betrieb muss bei der Produktion von Elektroartikeln mit Fixkosten von 2,5 GE sowie variablen Kosten von 0,5 GE rechnen. Er erzielt Erlöse gemäß der Funktion E mit E(x)=-0,5x^2+3,5x, wobei x den Absatz in ME angibt.

Bestimmen Sie die Funktionsgleichungen der Kosten- und Gewinnfunktion.
Zeichnen Sie die Graphen der Kosten-, Erlös- und Gewinnfunktion in ein Koordinatensystem. Bestimmen Sie zeichnerisch und rechnerisch die Gewinnzone.
Ermitteln Sie das Gewinnmaximum.

Mit einem Rechnungsweg wäre es sehr hilfreich für meine Prüfung!

Answer 1

durch die variablen und die Fixkosten ergibt sich die Kostenfunktion

K(x) = 0,5x +2,5

Gewinnfunktion G(x) = E(x) - K(x)

$$G(x)=-0,5x^2+3,5x-(0,5x+2)\\=0,5x^2+3,5x-0,5x-2,5\\=-0,5x^2+3x-2,5$$

Die Gewinnzone wird berechnet, indem man G(x) = 0 bestimmt. Daraus ergibt sich x₁ = 1 und x₂ = 5.

Das Gewinnmaximum erhältst du durch G'(x) = 0, also

-x + 3 = 0 ⇒ x = 3

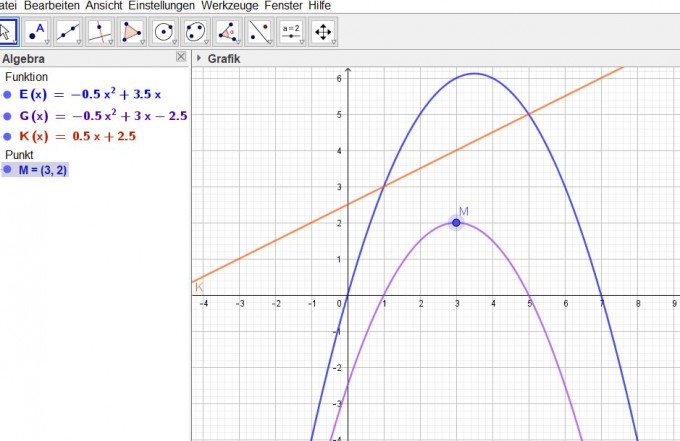
Gruß, Silvia