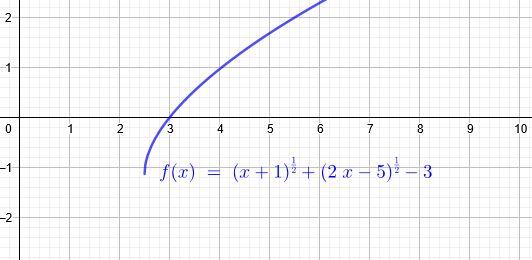
\( \sqrt{x+1} +\sqrt{2x-5}=3|^{2}\)
\( x+1 +2x-5+2 \sqrt{x+1} \sqrt{2x-5}=9\)
\( 3x+2\sqrt{(x+1)(2x-5)}=13\)
\( 2\sqrt{2x^2-3x-5}=13-3x|^{2}\)
\( 8x^2-12x-20=169-78x+9x^2\)
\(x^2-66x=-189 \)
\((x-33)^2=900 |±\sqrt{~~} \)
1.)
\(x-33=30 \)
\(x_1=63 \)
2.)
\(x-33=-30 \)
\(x_2=3 \)
Probe, weil Quadrieren keine Äquivalenzumformung ist.
1.) \( \sqrt{63+1} +\sqrt{121}≠3\)
2.) \( \sqrt{3+1} +\sqrt{6-5}=3\)✓