Hallo Fiona,
es folgt die ausführliche Antwort:
Um den Krümmungskreis in einem Punkt \(P\) an eine Parabel graphisch zu konstruieren, muss ihr Brennpunkt \(F\) und ihre Leitlinie bekannt sein.
"Eine Parabel ist der Ort aller Punkte, die von einem Punkt (dem Brennpunkt \(F\)) und einer Geraden (der Leitlinie \(l\)) gleich weit entfernt sind" (->
de.wikipedia.org/wiki/Parabel)
Bei einer Normalparabel liegt \(F\) bei \((0 \space \frac14)^T\) und die Leitline ist der Graph der Funktion \(y=-1/4\). Im folgenden Bild habe ich eine Parabel mit Leitlinie \(l\) (beide blau) und Brennpunkt \(F\) eingezeichnet.
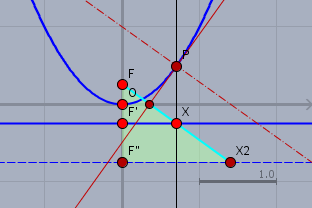
Ich wähle einen Punkt \(P\) auf der Parabel, fälle das Lot (schwarz) auf \(l\), welches \(l\) im Punkt \(X\) schneidet. Die Mittelsenkrechte (rot) der Strecke \(FX\) schneidet das Lot wiederum in \(P\) und diese Mittelsenkrechte ist auch gleichzeitig die Tangente an der Parabel in \(P\). In \(P\) errichte ich nun das Lot (rot Strich-Punkt) auf der Tangente und es ist offensichtlich, dass sich der Mittelpunkt des Krümmungskreises auf dem Lot der Tangente befinden muss.
Ich erwähnte bereits, dass ich die Formel für die Krümmung graphisch umsetzen möchte. Die da lautet: $$r(x)= \left| \frac12 (1 + 4x^2)^{\frac32} \right|$$ Das \(x\) ist hier die Strecke \(|F'X|\), wenn \(F'\) der Fußpunkt von \(F\) auf \(l\) ist. Wenn man nun das Dreieck \(\triangle F'XF\) um den Faktor 2 streckt, so erhält man das markierte rechtwinklige Dreieck \(\triangle F''X_2F\). Nach Pythagoras ist $$|FF''|^2 + |F''X_2|^2 = |FX_2|^2$$
Die Strecke \(|FF''|\) ist gleich \(1\), da dies eine Normalparabel ist. Die Strecke \(|F''X_2| = 2 \cdot |F'X| = 2x\) wegen der Streckung um den Faktor 2. Und somit berechnet sich \(|FX_2|\) (hellblau) zu $$|FX_2| = \sqrt{ |FF''|^2 + |F''X_2|^2 } = \left( 1^2 + (2 \cdot x)^2 \right)^\frac12 = \left( 1 + 4x^2 \right)^\frac12$$
Damit haben wir bereits einen entscheidenden Teil an dem Term oben. Im nächsten Schritt wird diese Strecke quadriert. Es ist also eine Strecke zu konstruieren, die \(1+4x^2\) entspricht. Multiplikationen führt man graphisch aus, indem man z.B. ein Rechteck aus den beiden Faktoren zeichnet und anschließend das Rechteck so schert, dass eine Höhe zu \(1\) wird. Die Länge der senkrecht zur Höhe \(1\) stehenden Seite ist dann das Ergebnis.
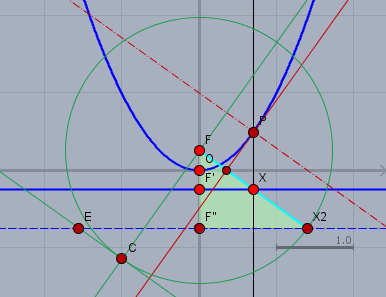
da \(|FX_2|\) quadriert werden soll, errichte ich das Lot (grün) in \(F\) und schlage mit dem Radius \(|FX_2|\) einen Kreis (grün) um \(F\), der das Lot in \(C\) schneidet. Die drei Punkte \(X_2\), \(F\) und \(C\) sind nun drei von vier Eckpunkten eines Quadrats mit der Fläche \(|FX_2|^2 = 1+4x^2\). Für die Konstruktion muss man das Quadrat nicht vervollständigen. Die Parallele zu \(FX_2\) durch \(C\) schneidet die Gerade \(l'\) (blau gestrichelt) durch \(FX_2\) in \(E\). Dies entspricht der Scherung des Quadrats, so dass die Höhe - in diesem Fall \(|F''F|\) - \(=1\) ist. Die Punkte \(X_2\), \(F\) und \(E\) sind nun drei von vier Eckpunkten eines flächengleichen Parallelogramms. Somit entspricht die Strecke $$|EX_2| = |FX_2|^2 = 1 + 4x^2$$
In genau der gleichen Weise 'multipliziert' man nun \(EX_2\) wieder mit \(FX_2\).

dazu trage ich die Strecke \(EX_2\) auf dem Lot (grün) in \(F\) ab (gelber Kreis) und erhalte den Punkt \(G\). \(X_2\), \(F\) und \(G\) sind wieder drei von vier Punkten eines Rechtecks mit dem Flächeninhalt von \(|FX_2| \cdot |EX_2| = |FX_2|^3\). Der Punkt \(G\) wird parallel zu \(FX_2\) geschert und man erhält den Punkt \(H\). Nun ist $$|HX_2| = |FX_2| \cdot |EX_2| = |FX_2|^3 = (1+4x^2)^{\frac32}$$
Jetzt muss man die Strecke \(|HX_2|\) nur noch halbieren; die Mitte ist \(M\) und schlägt einen Kreis (gelb gestrichelt) mit dem Radius \(MX_2\) um P, der das Lot (rot Strich-Punkt) im Krümmungsmittelpunkt \(K\) schneidet. Der Kreis (hell grün) um \(K\) durch \(P\) ist der gesuchte Krümmungskreis.
Da alle Parabeln ähnlich sind, unterscheidet sich die Konstruktion bei anderen Parabeln in keiner Weise! Man nimmt immer das doppelte der Strecke \(FF'\) als den Wert \(1\) an - quasi als Längenreferenz.
Gruß Werner