Beweis anhand eines Graphen zulässig? 1/2(x + 0.5x)≥1, für alle x Element R^+

Question

Es gilt zu beweisen, dass folgende (Un-)gleichung stimmt:

$\frac{1}{2}\left(x+\frac{1}{2} x\right) \geq 1$, für $\forall x \in R^{+}$

Nun hab ich mich an die Aufgabe gesetzt und bin auf folgendes gekommen:

$x^{2}+1 \geq 2 x$

Nach kurzer Überlegung ist mir aufgefallen, dass es sich dabei um - in Bezug auf die Zeichnung - ganz einfache Funktion handelt. Also habe ich mir beide vorgestellt und bin zu der Erkenntnis gekommen, dass die Aussage stimmt und sich beide Funktionen in B(1|2) berühren, siehe hier:

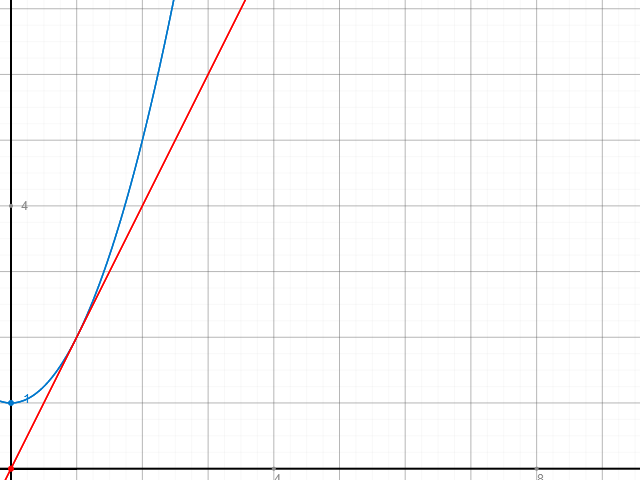
Die goldene Frage ist natürlich nun: Ist eine Zeichnung als Beweis zulässig? Denn es wird ja eigentlich recht deutlich veranschaulicht, dass die Aussage stimmt, oder nicht?

Answer 1

Da kann etwas nicht stimmen oder

1/2 * (x + 1/2 * x) ≥ 1

1/2 * (3/2 * x) ≥ 1

3/4 * x ≥ 1

x ≥ 4/3


Vielleicht so

1/2 * (x^2 + 1/2 * x) ≥ 1

x^2 + 1/2 * x ≥ 2

x^2 + 1/2 * x - 2 ≥ 0

x ≤ -1.686140661 ∨ x ≥ 1.186140661

Comments

Argh, mein Fehler. 'Tschuldigung es sollte natürlich heißen 1/2(x+1/x) >= 1.

Editieren geht jetzt auch nicht mehr. -.-

Aber Kern der Frage ist ja, ob eine Zeichnung als Beweis gültig ist.

Dennoch Danke für die schnelle Antwort.

---

1/2 * (x + 1/x) ≥ 1

x + 1/x ≥ 2

für x > 0

x² + 1 ≥ 2x

x² - 2x + 1 ≥ 0

(x - 1)² ≥ 0

Für alle x erfüllt. 

Daher ist die Gleichung für x > 0 erfüllt.

---

Zwar nicht das was ich genau wissen wollte, trotzdem eine Lösung für mein Problem.

Vielen Dank :D

---

An der Zeichnung kannst du nicht ablesen, dass der blaue Graph nicht vielleicht doch ein 2 Millionstel mm unterhalb des roten Graphen verläuft. Das kann man nur rechnerisch.

---

Ich schließe an die obige Gleichung an:

(x - 1)² ≥ 0

x - 1 ≥ 0

   x ≥ 1

Damit hast du deinen Beweis.

---

Die Gleichung

(x - 1)² ≥ 0

ist für alle x erfüllt und nicht nur für x ≥ 1.