Aufsuchen von Polynomfunktionen / Steckbriefaufgaben

Question

Aufgabe:

Der Graph einer Polynomfunktion vom Grad 3 besitzt den Hochpunkt H=(0/2) und den Tiefpunkt T=(4/-30). Ermittle eine Termdarstellung der Funktion f sowie den Wendepunkt des Graphen von f!

Problem/Ansatz:

Ich hab die Aufgabe nun mehrmals durchgerechnet und ich krieg sie einfach nicht gebacken. Bevor ich die nicht gelöst habe und meinen Fehler nicht checke geht garnix mehr... Ist jemand so lieb und schaut mal drüber was ich da falsch gemacht habe...Bitte... wenns geht bitte mit einer genauen Erklärung wo der Fehler liegt. Dankeee :)

Die richtige Lösung laut Lösungsbuch ist: f(x)= x³ – 6x² + 2; WP=(2/–14)

Comments

In der Aufgabenstellung steht, dass ein Hochpunkt in (0|2) existiert, du rechnest aber mit (0|3).

Außerdem weißt du ja schon, dass dein c=0 ist. Also setze doch direkt null ein (bzw. lasse es weg). Dann ist die Matrix übersichtlicher bzw. erhältst möglicherweise sogar ein LGS mit nur 2 Unbekannten.

---

Sehr geil - heute bin ich ja total Banane...

---

Wenn der HP tatsächlich in (0|3) wäre, würde deine Funktionsgleichung sogar stimmen.

---

Das ist wenigstens ein kleiner Trost für mich! Danke für die schnelle Antwort und schönen Abend dir! LG

Answer 1

damit die offene Frage geschlossen wird:

f(x)= ax³ + bx² + cx + d

f(0) = 2            (das ist wohl dein einziger Fehler!)
f(4) = -30
f '(0 )= 0
f '(4) = 0

ergibt das LGS

d = 2
64a + 16b + 4c + d = -30
c = 0
48a + 8b + c = 0

Einsetzen von d und c
64a + 16b + 2 = -30  ⇔  64a + 16b = -32  (G1)
48a + 8b  = 0              ⇔      6a +  b  =  0    ⇔ b = - 6a

b in G1:    64a - 96a = - 32  ⇔  -32a = - 32  ⇔  a = 1  →  b = - 6

f(x) =  x³ - 6·x² + 2 

Für spätere Kontrollen solcher Aufgaben kann ich dir diesen Online-Rechner empfehlen:

https://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

Gruß Wolfgang

Comments

Danke auch Dir Wolfgang! Die Seite ist der Hammer - hab sie gerade ausprobiert,

---

immer wieder gern :-)

Answer 2

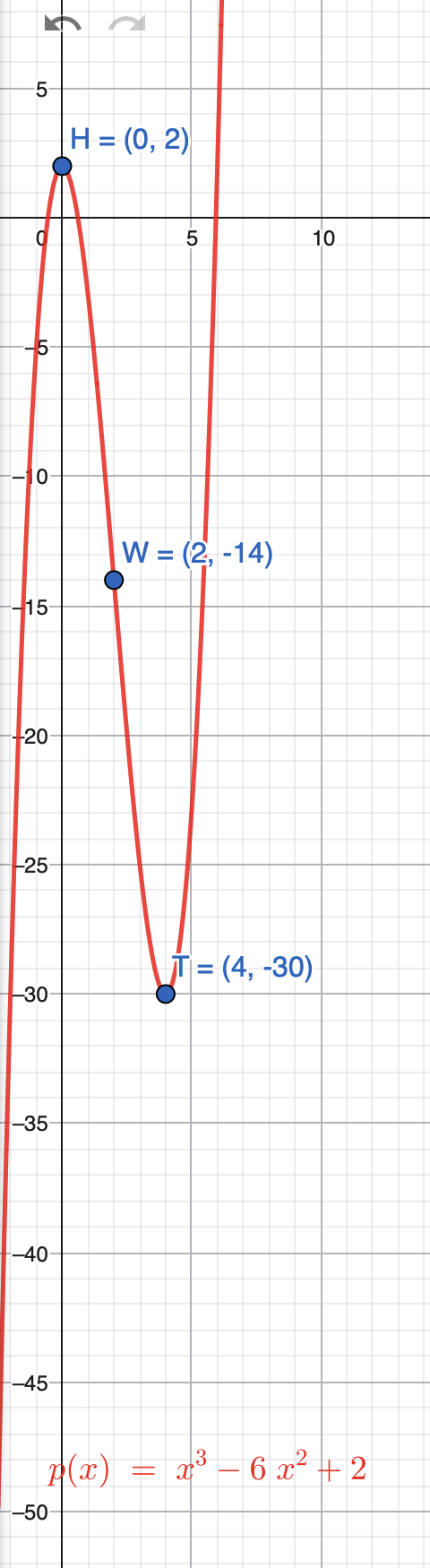
Der Graph einer Polynomfunktion vom Grad 3 besitzt den Hochpunkt H=(0|2) und den Tiefpunkt T=(4|-30). Ermittle eine Termdarstellung der Funktion f sowie den Wendepunkt des Graphen von f!

Ich verschiebe den Graph um   2 Einheiten nach   unten.

H=(0|2) → H´=(0|0)Der Graph hat im Extremum eine zweifache Nullstelle.

Linearfaktorenform:

\( f(x)=ax^2(x-N)=a(x^3-Nx^2)\)     T=(4|...) 1. Ableitung:

\( f'(x)=a(3x^2-2Nx)\)

\( f'(4)=a(48-8N)=0\)

\( N=6\)

\( f(x)=a(x^3-6x^2)\)       T=(4|-30)→ T´=(4|-32)

\( f(4)=a(64-96)=a(64-96)=-32a=-32\)

\(a=1\)

\( f(x)=x^3-6x^2\) Nun um 2 Einheiten nach oben:

\( p(x)=x^3-6x^2+2\)   

...sowie den Wendepunkt des Graphen:

\( f'(x)=3x^2-12x\)

\( f''(x)=6x-12\)

\( 6x-12=0\)

\( x=2\)   \( p(2)=8-24+2=-14\)

\( W(2|-14)\)