Ich versteh nicht genau wie ich hier vorgehen soll.
Du könntest Dir ja überlegen, was die Drehmatrix tut. Wenn Du einen beliebigen Punkt \(P\) nimmst, und die Matrix und den Punkt multiplizierst, so bekommst Du einen neuen Punkt \(P'\), der aus einer Drehung um eine noch unbekannte Drehachse resultiert. Mache das mal mit $$P = \begin{pmatrix} 1\\ 0\\ 0\end{pmatrix} \quad \to M \cdot P = \begin{pmatrix}-1 \\ 0\\ 0 \end{pmatrix} = P'$$Führst Du die Drehung mit \(P'\) noch einmal durch, so kommt wieder \(P\) heraus. Wenn Du das mit einem beliebigen anderen Punkt machst, geschieht das selbe. Nach zwei Multiplikationen landet man wieder beim ursprünglichen Punkt.
Was geht hier vor sich? Es ist anscheinend eine Drehung um 180°.
Das würde aber auch bedeuten, dass der Mittelpunkt von \(P\) und \(P'\) auf der Drehachse liegt. Der Mittelpunkt von \(P\) und \(P'\) ist aber der Ursprung, und der liegt immer auf der Drehachse. Ok - dann probiere einen zweiten Punkt$$Q = \begin{pmatrix} 0\\ 1\\ 0\end{pmatrix} \quad \to M \cdot Q = \begin{pmatrix}0 \\ -0,28\\ 0,96 \end{pmatrix} = Q'$$ Und der Mittelpunkt \(M_{QQ'}\) ist$$M_{QQ'} = \frac 12 \left( \begin{pmatrix} 0\\ 1\\ 0\end{pmatrix} + \begin{pmatrix}0 \\ -0,28\\ 0,96 \end{pmatrix}\right) = \begin{pmatrix} 0\\ 0,36\\ 0,48\end{pmatrix}$$Wir gehen also davon aus, dass die Drehachse durch den Ursprung \(O\) und durch \(M_{QQ'}\) geht - und damit können wir sie schon festlegen. Damit wir gefälligere Zahlen bekommen, multipliziere ich den Vektor \(\vec{OM_{QQ'}}\) mit \(100/12\) und erhalte die Drehachse \(d\) als Gerade:$$d: \space x = t \cdot \begin{pmatrix} 0\\ 3\\ 4\end{pmatrix}$$ Schau Dir die Szene in Geoknecht3D an:
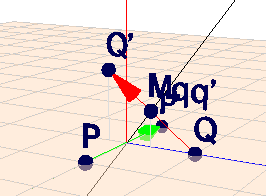
(klick auf das Bild, dann kannst Du die Szene mit der Maus drehen)
Falls das keine Drehung um 180° wäre, dann ginge die Drehachse nicht durch den Mittelpunkt von Punkt und gedrehtem Punkt. Aber in jedem Falle läge jeder Verbindungsvektor (grün und rot im Bild) in einer Drehebene, und diese steht immer senkrecht auf der Drehachse und damit auf jedem Vektor \(\vec{d}\) der Drehachse. Demnach gilt immer:$$\vec{PP'} \perp \vec{d}, \quad \vec{QQ'} \perp \vec{d}$$D.h. das Kreuzprodukt \(\vec{PP'} \times \vec{QQ'} = \vec{d}\) ist ein Vektor der Drehachse:$$\begin{pmatrix}-2 \\ 0\\ 0 \end{pmatrix} \times \begin{pmatrix}0 \\ -1,28\\ 0,96 \end{pmatrix} = \begin{pmatrix}0 \\ 1,92\\ 2,56 \end{pmatrix} = \frac{64}{100}\begin{pmatrix}0 \\ 3\\ 4 \end{pmatrix} $$Der Betrag spielt natürlich keine Rolle; es geht nur um die Richtung des Vektors.
Gruß Werner