f(x) = 2·x·e^{- 0.25·x^2}
f'(x) = e^{- 0.25·x^2}·(2 - x^2)
f''(x) = e^{- 0.25·x^2}·(0.5·x^3 - 3·x)
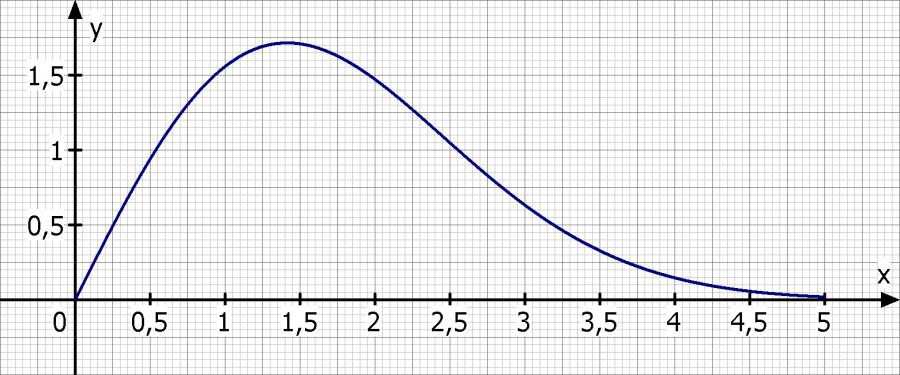
a) wie hoch ist ist die dammkrone?
Maximum f'(x) = 0
e^{- 0.25·x^2}·(2 - x^2) = 0
Da die e-Funktion nicht null werden kann, braucht nur die Klammer null werden.
2 - x^2 = 0
x = √2
f(√2) = 2·√2·e^{- 1/2} = 1.72 m
b)
Schreib dir dazu einfach e^{- 0.25·x^2} und leite es ab. Und dann frag dich, was du verändern musst um auf f(x) zu kommen.
F(x) = - 4·e^{- 0.25·x^2}
c) Irgendwie sehe ich hier ja nur den Damm eines Kanals aber nicht den wirklichen Kanal.
d)
Wendepunkt f''(x) = 0
e^{- 0.25·x^2}·(0.5·x^3 - 3·x) = 0
x = √6 ∨ x = 0
arctan(f'(√6)) = arctan(-0.8925206405) = -41.75°
Damit liegt die maximale Steigung etwa über 40°