Komplexe Gleichung z^2 + 24 + 10*i = 0. Alle Lösungen?

Question

Aufgabe:

Meine Aufgabe ist es alle komplexen Lösungen der Gleichung  z^2 + 24 + 10*i = 0 zu finden.

Problem/Ansatz:

Mein Ansatz wäre es umzuschreiben in z^2 = -24 -10i.

Dann z^2 umzuwandeln in (x^2 -y^2) + 2xyi.

Und dies dann in ein nicht-linares Gleichungssystem einzuführen

        1.  x^2 - y ^2 = -24

        2. 2xy = -10

Leider komm ich ab diesem Punkt nicht mehr weiter :(

Freue mich auf eine Antwort :D

Answer 1

1.  x^2 - y ^2 = -24

 2. 2xy = -10

Erste Variante. Faktorisieren und vereinfachen:

1.  (x-y)(x+y) = -24

 2. xy = -5

Nun systematisch probieren. Du erwartest zwei Lösungspaare (x,y) und findest diese sofort.

[spoiler]

-5 = - (1 * 5)

Nun die 1. Gleichung ansehen. Sowohl ( x=1 und y = -5 )  als auch (x=-1 und y = 5) passt bei 1.

Kontrolle mit:

https://www.wolframalpha.com/input/?i=x%5E2+-+y+%5E2+%3D+-24++,+2xy+%3D+-10

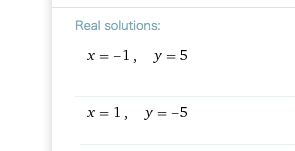
[/spoiler]

Zweite Variante: Einsetzmethode:

1.  x^2 - y ^2 = -24

2. 2xy = -10  ==> y = -5/x einsetzen in 1.

x^2 - ((-5)/x)^2 = - 24         | * x^2

x^4 - 25 = - 24x^2

x^4 + 24x^2 - 25 = 0.  | Faktorisieren oder z = x^2 substituieren und eine quadratische Gleichung lösen.  

Die blaue Methode dauert länger, führt aber sicher zum Ziel.

Faktorisieren ist schneller, wenn du im Kopf gut rechnest.

Comments

Boah, Vielen Dank!!

Sehr gut erklärt :)

---

Bitte. Gern geschehen!

Rechne das aber unbedingt noch selbst durch.

---

Hab ich gemacht und passt alles :D

Jetzt häng ich bei der nächsten Aufgabe fest, weil ich nicht weiß, wie man die Wurzel aus -24 - 10 i zieht :(

---

wie man die Wurzel aus -24 - 10 i zieht :(

Löse die Gleichung z^2 = -24 - 10i.

Alternative: Quadriere die beiden Resultate der obigen Aufgabe und staune.

[spoiler]

( 1 - 5i)^2 = 1 - 2* 5i + 25i^2 = -10i - 24

(-1 + 5i)^2 = 1 + 2*(-1)*5i + 25i^2 = -10i - 24

Somit sind die Wurzeln von -24 - 10i die Zahlen z_1= 1 - 5i und z_2 = -1 + 5i.

---

Danke, werd ich versuchen :)