Fouriertransformation g(t) = sin(πt) / (πt), t ≠ 0 , und g(0):= 1

Question

leider komme ich bei folgender Aufgabe nicht weiter.

Aufgabenbeschreibung:

Ein unbearbeitetes Signal ist durch Rauschen gestört und soll mit folgender Funktion im Zeitbereich gefaltet werden:

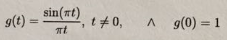
g(t) = sin(πt) / (πt), t ≠ 0 , und g(0):= 1

Aufgabe:

1. Handelt es sich um einen linearen Filter? Wenn ja welcher?

2. Berechnen Sie die Übertragungsfunktion.

3. Amplitudenspektrum skizzieren.

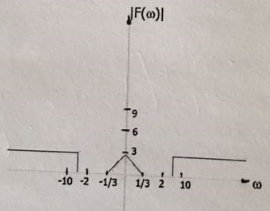
4. Wie sieht die idealisierte Wirkung des Filters auf das Eingangssignal mit folgendem Amplitudenspektrum aus? Skizzieren Sie das Spektrum von dem gefilterten Signal (idealisiert).

Problem/Ansatz:

Bei dieser Aufgabe weiß ich leider absolut nicht wie ich überhaupt anfangen soll bzw. ob das was ich vor habe richtig ist.

Als erstes stellt sich mir die Frage was es mit der Faltung in dieser Aufgabe auf sich hat?

Für eine Faltung benötige ich meines Wissens nach 2 Funktionen, ich habe aber nur eine! (?)

zu 1:

Es handelt sich um einen linearen Tiefpassfilter, da der Grenzwert bei zunehmenden w gegen 0 verläuft.

zu 2:

Mein Ansatz wäre die funktion g(t) mittels Fouriertransformation in G(w) zu transformieren.

D.h. G(w) = 1 / (2pi) * Integral von -unendlich bis +unendlich * g(t) * e^(-jwt) dt

zu 3:

Amplitudenspektrum zeichnen indem ich Werte für w in G(w) einsetze.

zu 4:

Was ist hierbei mit "idealisiert" gemeint? Wie wird das eingezeichnet?

Comments

Ein unbearbeitetes Signal ist durch Rauschen gestört und soll mit folgender Funktion im Zeitbereich ?? gefaltet werden:

g(t) = sin(πt) / (πt), t ≠ 0 , und g(0):= 1

Ist das alles, was du steht? Hast du eventuell ein paar Buchstaben im Text unterschlagen / andere Teilaufgaben / sonstigen Kontext aus den Unterlagen?

Bisher steht da nicht, ob g ein Signal oder das Rauschen ist. Könnte das Bild mit F ein Signal sein und g(t) das Rauschen? D.h. ich bin auch bei deiner Aussage:

Für eine Faltung benötige ich meines Wissens nach 2 Funktionen, ich habe aber nur eine! (?)

Hier mal ein Plot von g(x). 
~plot~ sin(π*x)/(π*x) ~plot~

Wenn der Zeitbereich konkret gegeben wäre und g das Signal, könnte man vielleicht daraus eine Faltung basteln. Vgl. mal mit https://www.nanolounge.de/16299/aufgabe-zur-diracfunktion-nachrichtentechnik

---

Hallo Lu,

die Aufgabenstellung ist folgendermaßen (1:1 abgetippt):

Ein Radio-Amateur hat festgestellt, dass, unbearbeitet, das von ihm empfangene Signal stark durch Rauschen gestört ist. Sein Nachbar, ein Mechatronik-Ingeneur, hat vorgeschlagen, es durch Anwendung der Fourier-Techniken abzuändern. Sein Vorschlag lautete, das Signal im Zeitbereich mit der Funktion g(t) (siehe oben) zu falten.

Analysieren Sie das Verhalten des so gefilterten Signals:

1. Handelt es sich um einen linearen Filter (Erklärung!) ? Wenn ja, um welche Filterart handelt es sich (Tiefpass, Hochpass, Bandpass)? Berechnen Sie die Übertragungsfunktion!

2. Skizzieren Sie das Amplitudenspektrum der Übertragungsfunktion.

3. Wie sieht die idealisierte Wirkung des Filters auf das Eingangssignal mit folgendem Amplitudenspektrum (S. Bild. Achtung: logarithmische Skalierung der w-Achse!)? Skizzieren Sie das Spektrum von dem gefilterten Signal (idealisiert!)!

Ich dachte auch schon, dass F(w) etwas mit g(t) bzgl. der Faltung zu tun haben könnte aber weiter komme ich an dieser Stelle auch nicht.

Wenn dies der Fall wäre müsste ich entweder g(t) transformieren und mit F(w) multiplizieren oder F(w) Rücktransformieren und mit g(t) multiplizieren? Seh ich das richtig?

Eine zweite Vermutung wäre, dass die g(t) das Signal ist und mit einer Funktion gefiltert wurde und F(w) rauskommt. D.h. ich müsste die Funktion ausrechnen mit der g(t) gefiltert wurde.

Vielen Dank im voraus für die Unterstützung!

---

Ihr habt offenbar gerade simultan reagiert. Danke für die vollständige Fragestellung. Ich hätte mir nachdem ich den oben angegebenen Link gefunden hatte, etwas in der Richtung erwartet, wie das ullim jetzt gemacht hat. Da dort ein Tiefpass herauskommt, scheint das zu deiner Frage zu passen. Studiere du mal, die Interpretation, die ullim da gemacht hat.

In der Wikipedia findest du drei Arten von charakteristischen Funktionen χ https://de.wikipedia.org/wiki/Charakteristische_Funktion mit ihnen kannst du z.B. ein- und ausschalten und nur gewisse Gebiete berücksichtigen.

Answer 1

Hi, ich versteh das so. \( F(\omega) \) ist das Eingangssignal (meinetwegen mit Rauschanteil, s. Zeichnung) und \( G(\omega) =  \mathcal{F}\{g(t)\} \) ist der Filter mit dem das Eingangssignal gefiltert werden soll.

Die Fouriertransformation von \( g(t) \) ist

$$ \mathcal{F}\{g(t)\}(\omega) = \chi_{ [-\pi, \pi] }(\omega) $$ mit \( \chi_{[-\pi, \pi} ] \) ist eine Rechteckfunktion im Bereich \( [-\pi , \pi ] \) mit Höhe \( 1\)

Die Faltung des Signals im Zeitbereich entspricht einer Multiplikation der Signale im Frequenzbereich.

Das bedeutet, dass aus dem Eingangsspektrum alle Frequenzen unterhalb von \( -\pi \) und oberhalb von \( \pi \) rausgefiltert werden. Insofern ist der Filter ein Tiefpassfilter.

Von dem angegebenen Spektrum bleibt im Idealfall also nur das Dreieckssignal übrig. \( G(\omega) \) ist also ein idealer Tiefpass.

Comments

Hallo ullim,

danke für deine Hilfe, leider bin ich jedoch mit der Antwort etwas überfordert..

Wie kommst du auf

für die Fourier transformierte von g(t)?

Das Problem was ich aktuell bei mir sehe, dass ich das Thema anscheinend nicht richtig verstanden habe und mir Beispiele fehlen um dies richtig zu verstehen.

G(w) hätte ich mit  \( \frac{1}{2*pi}  \int\limits_{-\infty}^{\infty} \)  \( \frac{sin(pi*t)}{pi*t} *e^{-jwt} dt \) berechnet.

Das ist die Formel für die Fouriertransformation in meinen Unterlagen.

---

Hi,

$$ g(t) = \frac{  \sin(\pi t) }{ \pi t  } = \frac{ e^{i \pi t} - e^{ -i \pi t  } }{  2 i \pi t } = \frac{1}{2 \pi} \int_{-\pi}^\pi e^{i t \omega} d\omega  = \mathcal{F}^{-1}\{ \chi_{[-\pi, \pi} \} $$

Also $$  \mathcal{F}(g) = \chi_{ [-\pi, \pi] } $$ Den Faktor \(\sqrt{ \frac{\pi}{2} } \) hatte ich fälschlicherweise davor geschrieben. Habe den Fehler korrigiert.

---

Danke dir!

und Lu natürlich auch :)