Question

Mehrstufige Zufallsversuche: Glücksrad mit Zahlen 9, 9, 7, 1, 9 usw. vgl. Bild. korrigieren bitte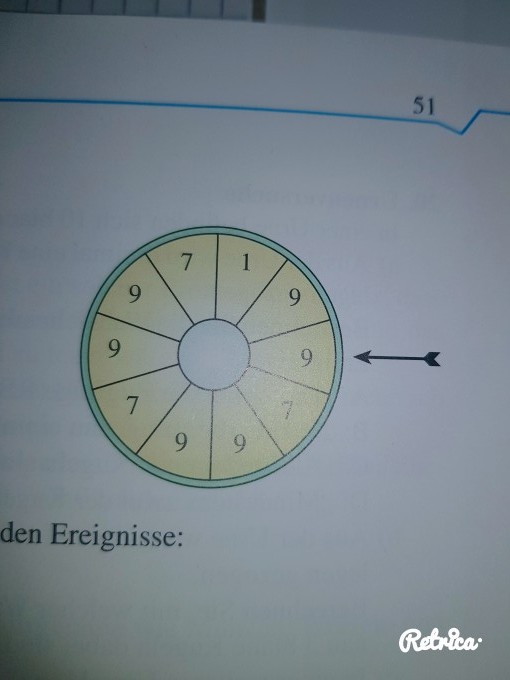 Guten guten Abend ich habe gerade eine Aufgabe gelöst, aber ich weiß nicht ob ich das richtig gemacht habe.

Die Aufgabe lautet: bei dem abgebildeten Glücksrad tritt jedes der 10 Felder mit der gleichen Wahrscheinlichkeit ein. Das Glücksrad wird zweimal gedreht a stellen Sie eine geeignete Ergebnismenge für dieses Zufallsexperiment auf und geben Sie die Wahrscheinlichkeiten aller Elementarereignisse mit Hilfe eines baumdiagramms an. Da habe ich für Gamma 9 raus

berechnen Sie die Wahrscheinlichkeiten der folgenden Ereignisse

A es tritt  höchstens einmal die 1 auf

B es tritt genau einmal die 7 auf

Cist tritt keine 9 auf

D=B geschnitten C

Bei A habe ich 18%, B 66%, C 72% da habe ich einfach das Gegenreignis gebildet bzw. gesagt, dass es eine 9 Auftritt oder muss ich -1 rechnen? D habe ich (1/10,3/10,6/10)

Comments

bei dem abgebildeten Glücksrad

Du müsstest uns schon beschreiben, was denn auf dem Rad abgebildet ist.

---

Ich habe ein Bild hinzugefügt

Answer 1

Ist dir klar, dass "höchstens eine 1" bedeutet, dass die 1

- in zwei Versuchen gar nicht kommt

oder

- nur im ersten Versuch kommt

oder

-nur im zweiten Versuch kommt?

Allein die erste der drei Varianten hat schon eine Wahrscheinlichkeit von 0,9*0,9=0,81 (das sind 81 %).

Und da kommen noch die Wahrscheinlichkeiten der anderen beiden Pfade dazu.

Überlege neu.

Answer 2

stellen Sie eine geeignete Ergebnismenge für dieses Zufallsexperiment auf

Ω = {'11', '17', '19', '71', '77', '79', '91', '97', '99'}

Da habe ich für Gamma 9 raus

Was ist Gamma?

Das Baumdiagramm könnte wie folgt aussehen:

Somit ist P('1) = 1/10, P('7') = 3/10, P('9') = 6/10 und demnach
P('11') = 1/10 * 1/10 = 1/100
P('17') = 1/10 * 3/10 = 3/100
P('19') = 1/10 * 6/10 = 6/100

usw.

Comments

So ist es vielleicht besser

---

Das ist ein großes Omega, kein Gamma.

Wenn du sagst, dass Omega gleich 9 ist, möchtest du ja ausdrücken, dass die Anzahl der Elemente, die in dieser Menge enthalten sind gleich 9 ist. Bitte setze dann Betragsstriche um Omega.

|Ω| = 9

A: Höchstens 1x die '1':
Wie abakus bereits geschrieben hat gibt es die Möglichkeiten

'1' - keine '1';     keine '1' - '1';        keine '1' - keine '1'

Hierfür lautet die WSK: P = 1/10 * 9/10  +  9/10 * 1/10  +  9/10 * 9/10 = 0.99