Eigenmann: Aufgabe #107, Teil 1

Question

Aufgabe:

Eigenmann-Aufgabe #107, Teil 1

Problem/Ansatz:

Ist die von E. genannte Lösung falsch ( vielleicht nur ein Druckfehler)?

Answer 1

Ist die von E. genannte Lösung falsch ( vielleicht nur ein Druckfehler)?

Um das zu beurteilen, müsste man wissen, was E. angegeben hat. Es gilt aber:

s = 1/2 * (80 + 85 + 85) = 125

r = √((125 - 80)(125 - 85)(125 - 85) / 125) = 24 cm

Was hat Eigenmann angegeben?

Comments

Ich finde es immer schön, wenn Schüler in der Lage sind, es einfach bei Geogebra zu skizzieren und zu kontrollieren.

---

E. gab das an, was Du ermittelt hast. Ich habe die schnell gefundene Höhe 75cm einfach gedrittelt. Ein offensichtlich bei mir eingebrannter Irrtum, das Drittel. Woher könnte dieser Irrtum stammen? Wann gilt Dritteln?

---

Es gilt aber:

s = 1/2 * (80 + 85 + 85) = 125

r = √((125 - 80)(125 - 85)(125 - 85) / 125) = 24 cm

Das finde ich eine schlechte Nachhilfe. Das Rechnen werden die Schüler schon können.

Was sie brauchen, ist ihnen die Formeln zu erklären.

---

In deiner Frage hast du nur gefragt, ob Eigenmann sich verrechnet oder vertippt hat. Ich habe dazu nur ein Kontrollergebnis zu berechnen, mit dem du vergleichen kannst.

Da ich nicht weiß, was du kennst und was nicht, musst du das schon mitteilen.

Kennst und verstehst du z.B. die Flächenformel von Heron?

A = √(s(s - a)(s - b)(s - c))

Siehe: https://de.wikipedia.org/wiki/Satz_des_Heron

---

Woher könnte dieser Irrtum stammen? Wann gilt Dritteln?

Die Seitenhalbierenden schneiden sich im Schwerpunkt, der die Seitenhalbierenden im Verhältnis 1:2 teilt.

Der Mittelpunkt des Inkreises ergibt sich aber als Schnittpunkt der Winkelhalbierenden.

Im gleichseitigen Dreieck sind die Seitenhalbierenden gleichzeitig auch die Winkelhalbierenden. Hier allerdings nicht.

---

Wenn schon beschränkter Aufwand Deinerseits, dann würde 24 cm² genügen, und ich gehe der Sache selbst weiter nach.  Meinen Fehler habe ich sofort erkannt. Über das, wie man es richtig macht, brauche ich inzwischen keine Nachilfe mehr. Aber ich würde es nett finden, eine Idee - wenn Du eine hast - beim Herausfinden meines eingebrannten Irrtums beizusteuern.

---

Über das, wie man es richtig macht

Die Aufgaben von Eigenmann zeigen doch wunderbar, dass es eben nicht den einen richtigen Weg gibt.

Aber ich würde es nett finden, eine Idee - wenn Du eine hast - beim Herausfinden meines eingebrannten Irrtums beizusteuern.

Lies halt seinen letzten Kommentar.

---

Da deine letzten beiden Aufgaben 1.107 und 1.140 beide aus der Gruppe sind, zu der Eigenmann als Tipp die Formel von Heron angegeben hat, habe ich dies zum Anlass genommen, die Formel auch eben hier anzuwenden, bzw. die Formel für den Inkreis, die unmittelbar auf der Formel von Heron beruht.

Answer 2

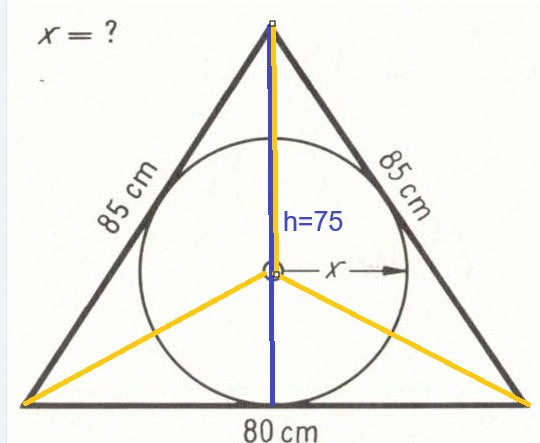
Nach dem Satz des Pythagoras gilt h=75 cm und somit A=0,5*75 cm * 80 cm = 3000 cm².

Berechnet man hingegen die Dreiecksfläche als Summe der orangefarbigen Teildreiecke, gilt

3000 cm² = 0,5*x*(85 cm + 85 cm + 80 cm).
(Der Inkreisradius ist in jedem der Teildreiecke die Höhe.)

Daraus ergibt sich x= 3000 cm²/(0,5*250 cm) = 24 cm.

Comments

Wieso begnügst Du Dich nicht mit dem, was erforderlich ist? Den ersten Satz und das hingegen finde ich überflüssig und nur irritierend

---

Wieso begnügst Du Dich nicht mit dem, was erforderlich ist?

Das ist immer schwer zu beurteilen, wenn man nicht weiß, was für den anderen jeweils erforderlich ist.

Daher ist es immer hilfreich, wenn Schüler ein eigenes Formel- und Merkheft führen, in dem die Formeln mit Herleitung drinstehen.

Dann ist das das Wissen, auf dem man aufbauen kann.

---

Und wer sagt, was erforderlich ist? Ich zumindest finde diesen Ansatz besser als den von MC, da er ohne Formeln auskommt, die man in der Regel nicht kennt oder lernt.

Weshalb sollte der erste Satz überflüssig sein? Zusammen mit diesem Satz macht auch das hingegen im darauffolgenden Satz durchaus Sinn. Man könnte auch die Worte einerseits und andererseits verwenden.

---

Wieso begnügst Du Dich nicht mit dem, was erforderlich ist? Den ersten Satz und das hingegen finde ich überflüssig und nur irritierend

Ich habe nun gerade versucht meinen (sehr elementaren) Ansatz auch denjenigen Personen zu erklären, die diesen nicht auf dem Schirm haben.

Tut mir leid wenn dich das irritiert hat.