Summenformel für Binomialkoeffizienten durch vollständige Induktion zeigen.

Question

Beweis durch Vollständige Induktion

∑_{von k=0 bis n}    (-1)^k / (k+1) * (n über k) = 1/(n+1)

(b) $\quad \sum \limits_{k=0}^{n} \frac{(-1)^{k}}{k+1}\left(\begin{array}{l}{n} \\ {k}\end{array}\right)=\frac{1}{n+1}$

Aufgabe:

Beweise, dass für alle n Elemente N gilt:  ∑ über k=0 bis n    (-1)^k/k+1 *  (n über k)=1/n+1

Problem/Ansatz:

∑Über k=0 bis n     (-1)^k / k+1 * n über k= ∑ über k=0 bis n    (n über k+1) = n! / (k+1)!*(n-(k+1)! = n! / k!(k+1)(n-k+1)! 

Ist der Ansatz schon mal richtig? Ich weiß nicht so genau, wie ich vorgehen soll.

Bin jedem dankbar.

Comments

Vom Duplikat:

Titel: Vollständige Induktion Summe

Stichworte: vollständige-induktion

Hallo ich würde mich sehr freuen wenn mir jemand sagen könnte wie diese Aufgabe funktioniert.

n

∑ ((-1)^k/k+1) ·(n über k)= $\frac{1}{n+1}$

k=0

---

Vom Duplikat:

Titel: Beweis mit binomischem Lehrsatz

Stichworte: binomischer-lehrsatz,binomialkoeffizient,beweis,vollständige-induktion,summenformel

Aufgabe: Beweise geschickt für n Element von N(0).

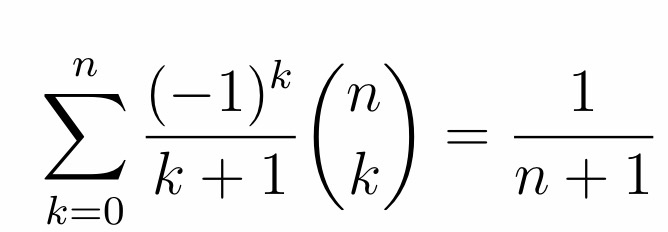
Als Hinweis wurde gegeben:

$\begin{pmatrix} x\\k \end{pmatrix}$ = $\frac{x}{k}$ * $\begin{pmatrix} x-1\\k-1 \end{pmatrix}$.

Sicherlich ist das geschickt auch auf den binomischen Lehrsatz bezogen.. Wie füge ich alle Teile zusammen?

---

Aloha :)

Diese Frage habe ich vor kurzem beantwortet, siehe:

https://www.mathelounge.de/663923/summenformel-binomialkoeffizienten…

---

Beim Duplikat gibt es schon eine Antwort. Vgl. unten.

Answer 1

Aloha :)

Sollst du das wirklich über vollständige Induktion beweisen? Das ist viel Schreiberei. Man kann den Beweis auch wie folgt direkt führen:

$$\sum\limits_{k=0}^{n}\frac{(-1)^k}{k+1}\binom{n}{k}=\frac{1}{n+1}\sum\limits_{k=0}^{n}(-1)^k\frac{n+1}{k+1}\binom{n}{k}=\frac{1}{n+1}\sum\limits_{k=0}^{n}(-1)^k\binom{n+1}{k+1}$$$$=\frac{1}{n+1}\sum\limits_{k=1}^{n+1}(-1)^{k-1}\binom{n+1}{k}=\frac{1}{n+1}\left[\sum\limits_{k=0}^{n+1}(-1)^{k-1}\binom{n+1}{k}-\underbrace{(-1)^{0-1}\binom{n+1}{0}}_{=(-1)}\right]$$$$=\frac{1}{n+1}\left[-\sum\limits_{k=0}^{n+1}(-1)^{k}\binom{n+1}{k}-(-1)\right]=\frac{1}{n+1}\left[1-\sum\limits_{k=0}^{n+1}\binom{n+1}{k}(-1)^{k}\cdot1^{(n+1)-k}\right]$$$$=\frac{1}{n+1}\left[1-(1-1)^{n+1}\right]=\frac{1}{n+1}$$

Comments

Ja, dürfen auch ohne vollständige Induktion. Vielen Dank für die Hilfe. Habe nachher meinen Fehler gesehen.