Vollständige Induktion Mit binomialkoeffizienten

Question

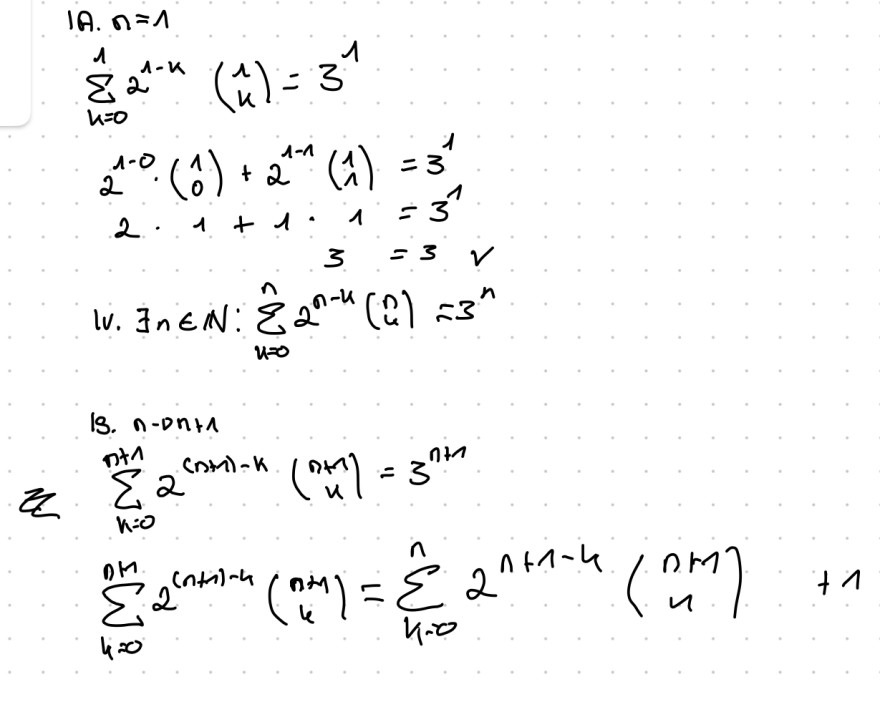
Text erkannt:

IA. \( n=1 \)
\( \begin{aligned} \sum \limits_{k=0}^{1} 2^{1-k}\left(\begin{array}{l} 1 \\ k \end{array}\right) & =3^{1} \\ 2^{1-0} \cdot\left(\begin{array}{l} 1 \\ 0 \end{array}\right)+2^{1-1}\left(\begin{array}{l} 1 \\ 1 \end{array}\right) & =3^{1} \\ 2 \cdot 1+1 \cdot 1 & =3^{1} \\ 3 & =3 v \end{aligned} \)
\( \text { Iv. } \exists n \in \mathbb{N}: \sum \limits_{u=0}^{n} 2^{n-u}\left(\begin{array}{l} n \\ u \end{array}\right)=3^{n} \)
18. \( n-0 n+1 \)
\( \begin{aligned} \sum \limits_{k=0}^{n+1} 2^{(n+1)-k}\left(\begin{array}{c} n+1 \\ k \end{array}\right) & =3^{n+1} \\ \sum \limits_{k=0}^{n m} 2^{(n+1)-k}\left(\begin{array}{c} n+1 \\ k \end{array}\right) & =\sum \limits_{k-0}^{n} 2^{n+1-k}\left(\begin{array}{c} n m \\ n \end{array}\right)+1 \end{aligned} \)

Aufgabe: Ziegen sie das für jede natürliche Zahl n> gleich 1 gilt:

n

∑2^(n-k) (n über K)= 3^n

k=0

Problem/Ansatz:

Induktionsanfang habe ich hinbekommen.Beim induktionsschritt weiß ich nicht weiter. Wenn ich n+1 einsetze, weiß ich nicht wie ich die +1 bei 2^(n+1)-k wieder los werde.

Answer 1

Im Pascalschen Dreieck gilt \( \begin{pmatrix} n\\k-1\end{pmatrix} \)+\( \begin{pmatrix} n\\k\end{pmatrix} \)=\( \begin{pmatrix} n+1\\k\end{pmatrix} \).

Das kannst du nutzen, um \( \begin{pmatrix} n+1\\k\end{pmatrix} \) durch das in der Induktionsvoraussetzung vorhandene \( \begin{pmatrix} n\\k\end{pmatrix} \) auszudrücken.

Comments

Um die IV einsetzen zu können, bräuchte ich ja die Form 2^n-k vor dem Binomialkoeffizienten.