Ich hatte nach dem missglückten Start heute morgen keine Zeit, jetzt aber:
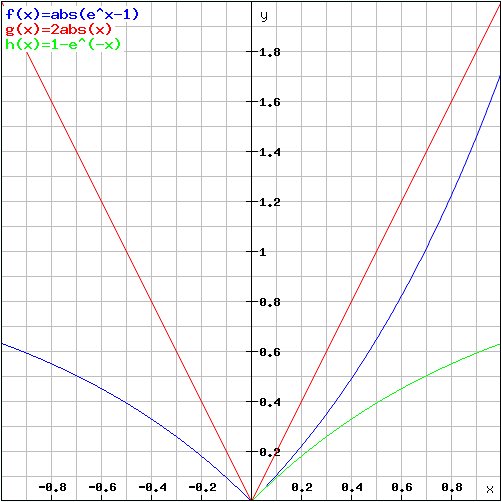
zu zeigen: blau ≤ rot im Intervall [-1,1], ob offen oder geschlossen ist egal!
Spiegele abs(e..) an der y-Achse. Die Aussage ist bewiesen, wenn die folgende Ungleichungskette gilt:
grün ≤ blau ≤ rot im Intervall [0,1]. Dadurch hat man keinen Ärger mit negativen Zahlen oder Beträgen.
z,z: 1 - e-x ≤ ex - 1 ≤ 2x im Intervall [0,1]
(1) 1 - e-x ≤ ex - 1 I *ex Ich mache es heuristisch durch Äquivalenzumformung, damit nachvollziehbar:
⇔ ex - 1 ≤ e2x - ex
⇔ 0 ≤ e2x - 2ex +1
⇔ 0 ≤ (ex -1)2 ok wegen ^2
(2) ex - 1 ≤ 2x im Intervall [0,1]
Die linke Seite ist f(x). Der Graph ist eine Linkskurve, weil die 2. Abl.≥ 0.
Also liegt der Graph unterhalb der Geraden zwischen dem Anfangspunkt (0,0) und dem Endpunkt (1,e-1).
Diese Ursprungsgerade hat die Steigung e-1≈2,7 und liegt damit unter der Ursprungsgeraden y = 2x mit dem Endpunkt (1,2). q.e.d
Jetzt mit Taylor:
z.z.: ex - 1≤ 2x im Intervall [0,1]
⇔ ex ≤ 1 + x + x im Intervall [0,1]
Bew: ex = 1+x+x2/2 + x3 * f''(ξ) / 6 mit ξ∈[0,x]
Nachweis, dass
x2/2 + x3 * f''(ξ) / 6 ≤ x
x2/2 + x3 * eξ / 6 ≤x2/2 + x3 * e1 / 6 ≤ x2/2 + x3 * 1 / 2 ≤ \( \frac{x^{2}}{2} \) (1 + x) ≤ x
stimmt, denn der vorletzte Term ist eine Funktion durch (0,0) und (1,1), deren Graph eine Linkskurve ist, die unterhalb der 1. Winkelhalbierenden liegt.