Hallo Tamara,
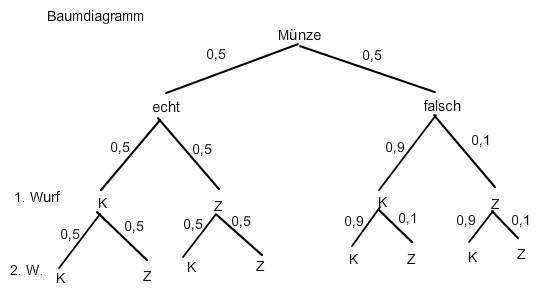
Bei jeder Frage musst du die Wahrscheinlichkeiten bei jedem Weg ("Pfad"), der zu dem gefragten Ereignis führt, multiplizieren und die Ergebnisse addieren:
a) P(1. Wurf K) = 0,5·0,5 + 0,5·0,9 = 0,7
b) P(2. Wurf K)
= 0,5·0,5·0,5 + 0,5·0,5·0,5 + 0,5·0,9·0,9 + 0,5·0,1·0,9 = 0,7
Warum sollten sich die beiden Wahrscheinlickeiten auch unterscheiden ?
c) Sei A = 2. Wurf K , B = 1. Wurf K
Es geht um die bedingte Wahrscheinlichkeit
P(A|B) = P(A∩B) / P(B) = ( 0,53 + 0,5·0,92) / 0,7 ≈ 0,757
Nachtrag:
d) die Ereignisse sind abhängig, sonst müsste P(A|B) = P(A) gelten.
Gruß Wolfgang