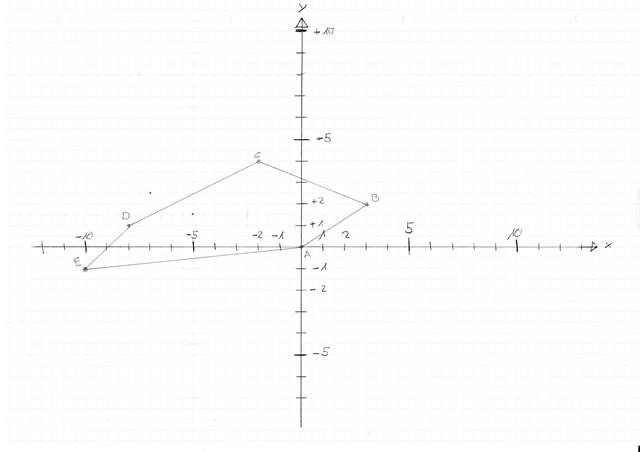
das Foto zu Aufgabe a)
Ich löse die Aufgabe b) mit orange:
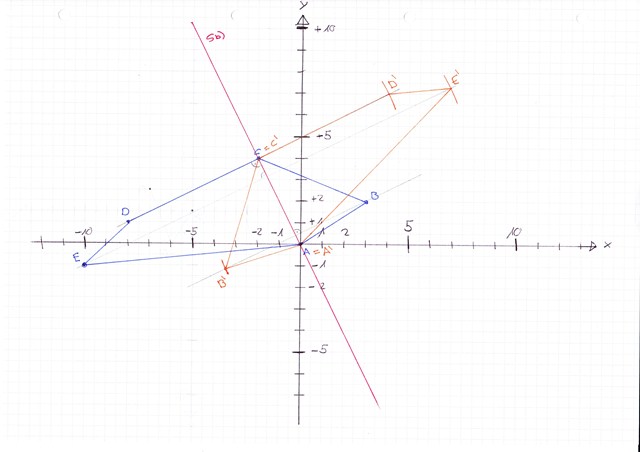
Dies war eine Achsenspiegelung an der roten Spiegelachse s. Man macht eine Senkrechte durch den Punkt, den man spiegeln will und nimmt den Abstand sPunkt den man spiegel will in den zirkel, dreht ihn um 180° und trägt dies auf der Senkrechten ab, wobei der Punk auf s der Punkt ist, indem die Senkrechte s schneidet.
Zu Aufgabe c). Hier zuerst das Bild:
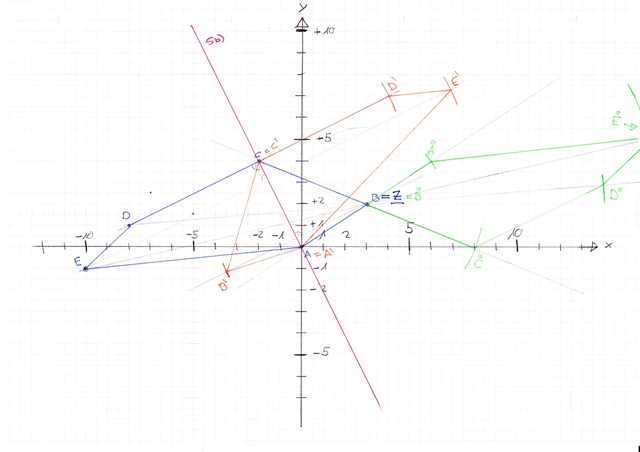
Bemerkung: Bei mir passte leider der Punkt E° nicht mehr aufs Blatt....
Du musst in diesem Fall B als zenrum Z nehmen. Danach verbindest du alle Punkte mit Z (und verlängerst deise Gerade). Jetzt wieder mit dem Zirkel die Figur umdrehen... Die Lösung ist grün.
Aufgabe d):
Ich kenne hier das Streckungszentrum nicht, deshalb lasse ich diese Aufgabe aus... Wenn du jedoch Z hast, dann kannst du wie in c) Die Strecke C'''D''' abtragen (du halbierst die Ausgangsstrecke und drehst sie mit der oben genannten Methode um, !!!dies jedoch beim Punkt C'''!!!). Danach kannst du alle Seiten einfach parallel verschieben (D''E'' durch D''' verschieben und die Hälfte abtragen, usw.).
Ich hoffe, ich konnte dir helfen und du verstehst es jetzt!
Simon