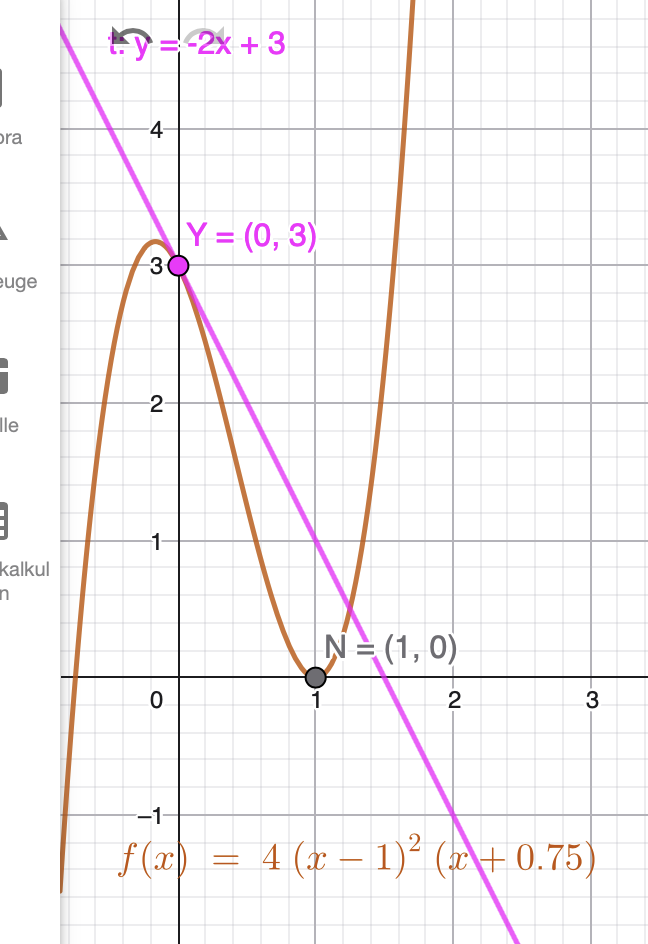
Für den Graph einer ganzrationalen Funktion 3. Grades ist für \( x=1\) die Achse eine Tangente. Auf der y-Achse liegt die Tangente t: y= -2x+3 an den Graphen an. Bestimme Sie das Polynom
...liegt die Tangente t: \( y= -2x+3\) an den Graphen an:
\( f(0)=3\) → Y \((0|3)\). Doppelte Nullstelle bei \( x=1\) Nullstellenform:
\( f(x)=a(x-1)^2(x-N) \)
...die Tangente t: y= -2x+3 an den Graphen an: \(m=-2 \)
\( f'(x)=a[(2x-2)(x-N)+(x-1)^2] \)
\( f'(0)=a[(-2)(-N)+(-1)^2]=a(2N+1)= -2 \)
\(a=-\frac{2}{2N+1} \)
\( f(x)=-\frac{2}{2N+1}(x-1)^2(x-N) \)
Y \((0|3)\):
\( f(0)=-\frac{2}{2N+1}(-N) =3\)
\( N=-0,75\)
\(a=-\frac{2}{-1,5+1}=4 \)
\( f(x)=4(x-1)^2(x+0,75) \)