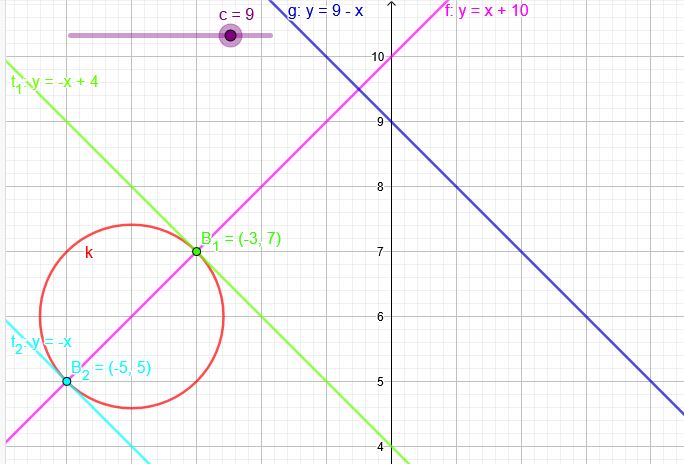
\((x + 4)^2 + ( y− 6)^2 = 2 \) \(y=c-x\) mit \(m=\red{-1}\)
\(k(x,y)=(x + 4)^2 + ( y− 6)^2 - 2 \)
\(k_x(x,y)=2(x + 4) \)
\(k_y(x,y)=2( y− 6) \)
\(k'(x)=-\frac{k_x(x,y)}{k_y(x,y)}=-\frac{x+4}{y− 6}\)
\(\red{-1}=-\frac{x+4}{y− 6}\)
\(y=x+10\) Diese Gerade schneidet den Kreis in den beiden Berührpunkten:
\((x + 4)^2 + ( x+10− 6)^2 = 2\)
\((x + 4)^2 + ( x+4)^2 = 2\)
\(2\cdot(x + 4)^2 = 2\)
\((x + 4)^2 = 1 |±\sqrt{~~}\)
\(1.)\)
\(x + 4 = 1 \)
\(x_1 = -3 \) \(y(-3)=-3+10=7\)
\(2.)\)
\(x + 4 = -1 \)
\(x _2= -5 \) \(y(-5)=-5+10=5\)
Tangentengleichungen:
\(1.)\):
\( \frac{y-7}{x+3}=\red{-1} \)
\( y=4-x \) \(c_1=4\)
\(2.)\):
\( \frac{y-5}{x+5}=\red{-1} \)
\( y=-x \) \(c_2=0\)