Mehrdimensionale Funktion auf Extrema in einem Gebiet untersuchen.

Question

Aufgabe:

Gegeben sei die Funktion f(x, y) = cos(x) sin(y) auf dem Gebiet (x, y) ∈ D := (0, 2π)²
a) Berechnen Sie den Gradienten ∇f(x, y) und die Hesse Matrix Hf (x, y) von f.
b) Bestimmen Sie alle Kandidaten für lokale Extrema von f im Inneren von D.

c) Klassifizieren Sie die kritischen Punkte: Handelt es sich um Maxima, Minima, oder Sattelpunkte?
Problem/Ansatz:

Den Gradienten und die Hessematrix zu berechnen war kein Problem, aber ich habe keine Ahnung, wie man Extrema in einem Bereich findet.

Wenn man den Gradienten 0 setzt, also in dem Fall sollte dies -(sin(x)*sin(y))=0  sein,

                                                                                                     cos(x)*cos(y)=0

komme ich auf x=0 und y=π/2 .

Bringt mir das was bzw. habe ich was falsch gemacht?

Oder ist das der Extrempunkt und ich soll ihn in die Hessematrix einsetzen um anschließend zu bestimmen ob es ein Minima/Maxima oder Sattelpunkt ist?

Aber dann nutze ich ja nicht das Gebiet.

Answer 1

Hallo Daniel,

das ist eine Extremwertaufgabe mit Nebenbedingung. Die Nebenbedingung ist in diesem Fall das Rechteck $D=[0,2\pi]\times [0,2\pi ]\subset \mathbb{R}$. Ich habe $f$ hier mit auf dem interessanten Definitionsbereich $D$ (in grün) dargestellt.

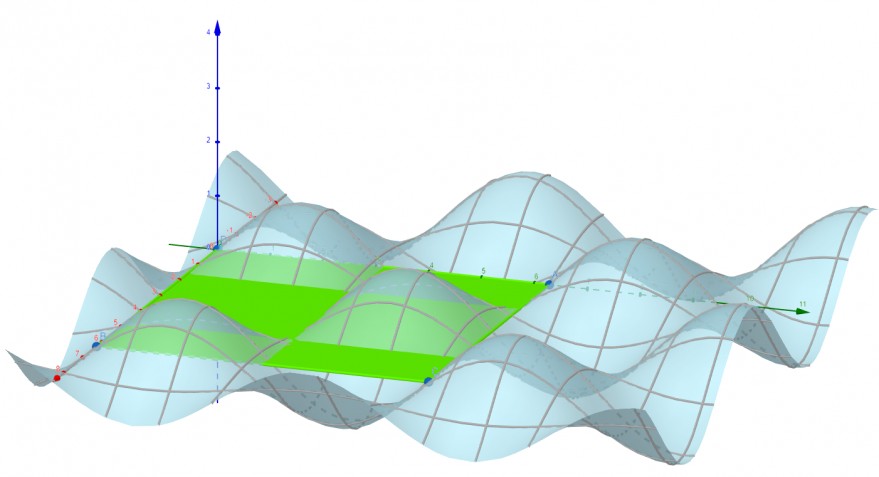
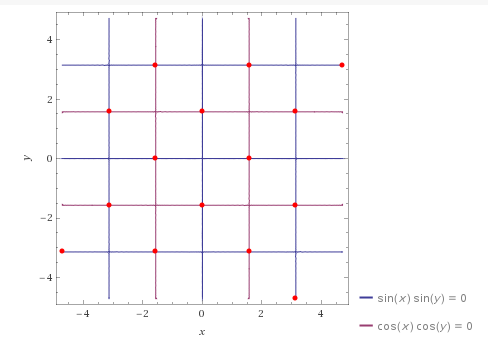
Du untersuchst zum einen das Innere $D^{\circ}$ vom Definitionsbereich - das machst du wie gewohnt ohne Beachtung des Definitionsbereichs. Also:$$\nabla f(x,y)=\begin{pmatrix} -\sin(x)\sin(y)\\\cos(x)\cos(y) \end{pmatrix}\overset{!}{=}\begin{pmatrix} 0\\0 \end{pmatrix}\Rightarrow \begin{cases}-\sin(x)\sin(y)=0 \\ \cos(x)\cos(y)=0\end{cases}$$ Hier wendest du den Satz vom Nulprodukt an. Es ist nämlich  $-\sin(x)\sin(y)=0 \Leftrightarrow \sin(x) \, \vee \sin(y)=0$. Hierbei ist $\sin(x)=0 \Leftrightarrow x_1=k\pi$ mit $k\in \mathbb{Z}$. Analog folgt, dass $y_1=k\pi$, ebenfalls mit $k\in \mathbb{Z}$. Nun analog mit $\cos(x)\cos(y)=0 \Leftrightarrow \cos(x)=0 \, \vee \, \cos(y)=0$ und das gilt genau dann, wenn $x_2=(k+0.5)\pi$ bzw. $y_2=(k+0.5)\pi$.

Du musst nun auf den Definitionsbereich achten und geeignete Punkte wählen. In Frage kommen z. B. $(0,\pi /2), (\pi.1.5\pi), (\pi,0.5\pi)$.

Um den Rand von $D$ zu untersuchen, nimmst du dir die Eckpunkte von $D$, also $(0,0), (0,2\pi),(2\pi,2\pi), (2\pi, 0)$, und verbindest diese zu einer Gerade, die du in $f$ einsetzt. Das ist dann eine Funktion mit einer Variable, die du auch separat auf Extrema untersuchen musst.

Comments

Vielen Dank für deine Mühe!

Hat mir sehr weitergeholfen :)

---

Kein Ding, wenn du Fragen hast, kannst du dich melden!