Hallo.
es folgen drei unterschiedliche Lösungen chronologisch, so wie sie mir eingefallen sind:
Das geht über die Eigenwerte und Eigenvektoren. Ich unterstelle, dass die Achse \(a\) der Parallelstreckung (die gegebene Gerade) eine Ursprungsgerade ist. Dann ist die Abbildung linear. Der erste Eigenvektor der gesuchten Matrix \(M\) ist die Richtung dieser Geraden \(a\) und der zugehörige Eigenwert muss \(=1\) sein. Das folgt aus der Vorgabe der Parallelstreckung, da jeder Punkt auf der Geraden \(a\) auf sich selbst abgebildet wird.
Der zweite Eigenvektor ist die Differenz \(P'-P\) (Bildpunkt minus Punkt). Und der zugehörige Eigenwert berechnet sich aus dem Verhältnis der Abstände \(P'\) zu \(a\) bezogen auf \(P\) zu \(a\).
Ein Beispiel:
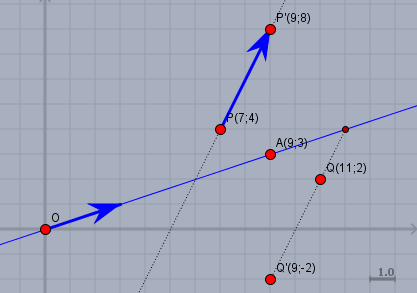
aus dem Bild kann man die Richtung der Geraden \(a\) (blau) ablesen:$$a = t \begin{pmatrix}3\\ 1\end{pmatrix} \implies \vec e_1 = \begin{pmatrix}3\\ 1\end{pmatrix}, \quad e_1 = 1$$und aus dem beiden Punkten \(P(7;4)\) und \(P'(9;8)\) folgt$$\vec e_2 = P'- P = \begin{pmatrix}2\\ 4\end{pmatrix}, \quad e_2 = \frac{\left< P',\, \vec e_1^{\perp}\right>}{\left< P,\, \vec e_1^{\perp}\right>} = \frac{15}{5} = 3$$Nun gilt es folgende Gleichung zu lösen, um die gewünschte Matrix \(M\) zu bestimmen$$ M \cdot \begin{pmatrix}\vec e_1& \vec e_2\end{pmatrix} = \begin{pmatrix}\vec e_1& e_2 \cdot \vec e_2\end{pmatrix}$$also hier$$M \cdot \begin{pmatrix}3& 2\\ 1& 4\end{pmatrix} = \begin{pmatrix}3& 6\\ 1& 12\end{pmatrix} \\ \implies M = \begin{pmatrix}0.6& 1.2\\ -0.8& 3.4\end{pmatrix}$$Überprüfe das bitte - z.B. mit dem Punkt \(A(9;3)\) (s. Bild oben), der muss auf sich selbst abgebildet werden oder mit dem Punkt \(Q(11;2)\), der auf den Punkt \(Q'(9;-2)\) abgebildet werden muss.
Falls Du noch Fragen hast, so melde Dich bitte.
Nachtrag:
mir ist gerade noch eingefallen, dass der Weg über die Eigenvektoren gar nicht nötig ist. Es reicht aus, eine Punkt \(A\) auf der Geraden \(a\) zu wählen und mit den Punkten \(P\) und \(P'\) folgendes Gleichungsystem zu lösen:$$\begin{aligned} M \cdot \begin{pmatrix}A & P\end{pmatrix}&= \begin{pmatrix} A & P' \end{pmatrix} \\ M \begin{pmatrix}9& 7\\ 3& 4\end{pmatrix} &= \begin{pmatrix}9& 9\\ 3& 8\end{pmatrix} \\ M &= \begin{pmatrix}9& 9\\ 3& 8\end{pmatrix} \cdot \frac {1}{15} \begin{pmatrix}4& -7\\ -3& 9\end{pmatrix} \\ &= \begin{pmatrix}0.6& 1.2\\ -0.8& 3.4\end{pmatrix}\end{aligned}$$das Ergebnis muss natürlich das gleiche sein!
und noch 'ne Lösung:
man kann die Matrix \(M\) auch direkt berechnen ohne eine andere Matrix invertieren zu müssen (obwohl das in 2D kein Problem ist!). Eine geschlossen Formel für \(M\) wäre: $$M = \underline 1 + \frac{k-1}{\left< \vec r , \, \vec a^{\perp}\right>} \vec r \vec a^{\perp T}, \quad \vec r = P'-P, \quad k = \frac{\left< P',\, \vec a^{\perp}\right>}{\left< P,\, \vec a^{\perp}\right>}$$\(k\) - der Faktor der Streckung - ist identisch mit dem zweiten Eigenwert \(e_2\) (s.o.). \(\vec a^\perp\) ist ein Vektor, der senkrecht auf \(\vec a\) steht. Im Beispiel oben ist \(\vec a^{\perp T} = \begin{pmatrix} -1& 3\end{pmatrix}\).
Bem.: ist \(k=-1\) und \(\vec r \perp \vec a\), dann handelt es sich um eine Spiegelung.