Hallo,
Auf dem Rand untersuchst du \(f(x,g(x))\) wobei \(g: [-1,1]\to \mathbb{R},\, g(x)=1-x^2\) und \(f(x,h(x))\) (siehe unten). Das sind eindimensionale Funktionen, die diejenigen Kurven beschreiben, wenn du dir vorstellst, du würdest eine der beiden Funktionen aus der \(x\)-\(y\)-Ebene in \(f\) einbetten.
Untersuche erst einmal ganz normal auf Extrema mittels Gradient =0 und Hessematrix usw. und schau, ob du vielleicht kritische Punkte in \(D\) findest, wenn sie außerhalb liegen, kannst du sie verwerfen.
Danach untersuchst du \(f(x,g(x))\) auch auf Extrema, das ist dann eine eindimensionale Funktion, die die Randkurve beschreibt. Außerdem musst du mit \(h: [-1,1] \to \mathbb{R}, x\mapsto 0\) auch \(f(x,h(x))\) betrachten.
PS:
Ich denke, dass die Bedingung \(0\leq y \leq 1-x^2\) die weitere Bedingung \(x\in [0,1]\) inkludiert und das somit redundant in der Menge noch einmal aufgeführt wird. Denn aus \(0\leq y \leq 1-x^2\) folgt transitiv, dass \(0\leq 1-x^2 \Leftrightarrow x^2\leq 1 \Leftrightarrow x\in [-1,1]\).
PSS:
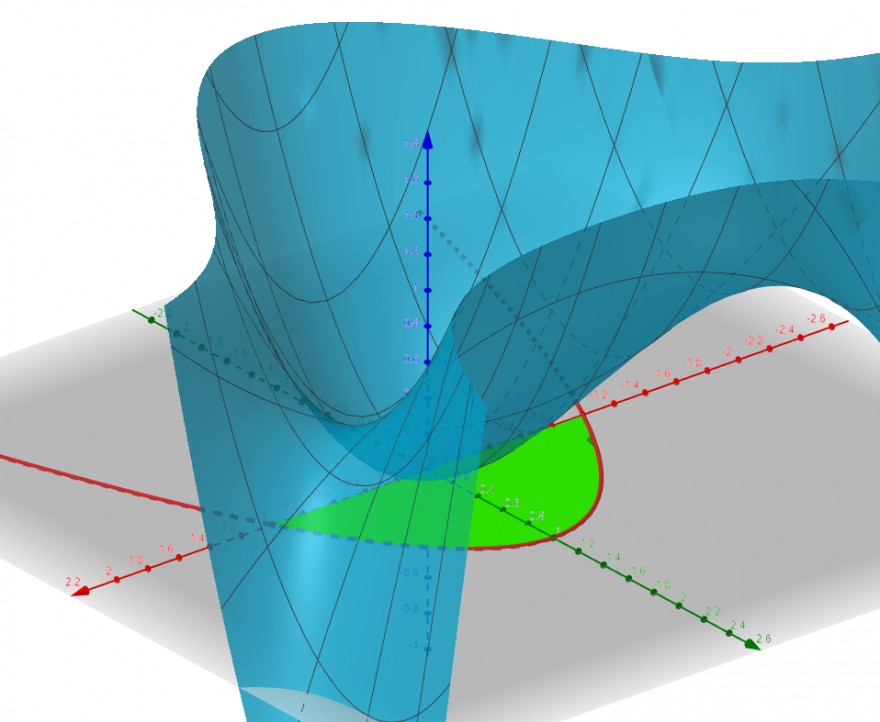
Die beiden Randfunktionen \(g\) und \(h\) beschreiben den Rand von \(D\), hier als Bild (h in blau und g in grün):