Hallo schnuckimucki,
.. aus der Wikipedia:
"In der euklidischen Geometrie versteht man unter einer Konstruktion mit Zirkel und Lineal die Entwicklung der exakten zeichnerischen Darstellung einer Figur auf der Grundlage vorgegebener Größen, wobei in der Regel nur Zirkel und Lineal verwendet werden dürfen. Das Lineal hat keine Markierungen; man kann damit also nur Geraden zeichnen, aber keine Strecken abmessen."
Bei dieser Aufgabe sind zwei Strecken vorgegeben. Die Seite AB und die Diagonale AC. Dass da ein Wert in der Aufgabestellung steht, mit Centimetern dahinter, ist lediglich eine Bequemlichkeit der Aufgabensteller. Gegeben ist genau genommen ...
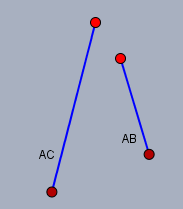
.. das hier. Mehr nicht!
Wähle einen Punkt M und ziehe einen kreis k(M,3,5cm)
Das geht nicht, da nirgendwo eine Strecke dieser Länge mit dem Zirkel abgegriffen werden kann. Die 3,5cm müssen erst durch Halbierung der Strecke \(AC\) konstruiert werden.
1. Zeichne die Strecke AC mit 7cm.
Besser: Zeichne eine Gerade, markiere einen Punkt \(A\) darauf und trage mit dem Zirkel die Strecke \(AC\) ab.
2. Ziehe um den Mittelpunkt M ...
\(M\) existiert doch noch gar nicht.
Also: 2. Konstruiere den Mittelpunkt \(M\) der Strecke \(AC\).
.. der Strecke einen Kreis k(M,4cm)
Du meinst 3,5cm. Ist aber auch falsch, da die 3,5cm nicht vom Himmel fallen.
Besser: 3. Schlage um \(M\) einen Kreis mit dem Radius \(MA\) (oder \(MC\))
Wichtig: Du kannst nur Dinge, Größen und Sätze benutzen, die Du schon hast. Das ist ein grundsätzliches Prinzip in der Mathematik und gilt für alle Bereiche auch außerhalb der Geometrie!
5. Ziehe einen weiteren kreis l sodass, l(C,4cm).
das ist zwar nicht falsch, aber im Nachgang mehrdeutig, wie man hier sieht:
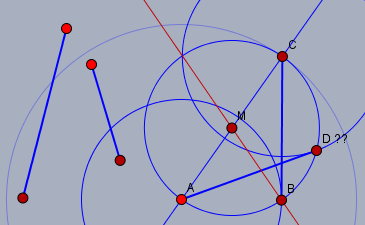
Nach der Konstruktion von \(B\) ist es besser (und einfacher), eine Gerade (rot) durch \(M\) und \(B\) zu zeichen, die den Kreis um \(M\) außer in \(B\) noch in \(D\) schneidet.