Aufgabe:
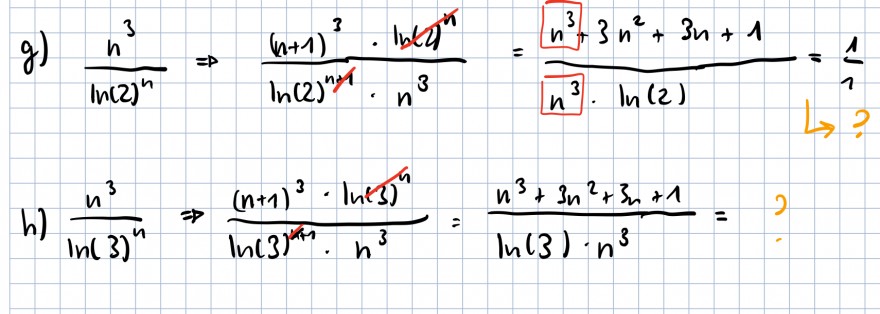
Text erkannt:
\( g)=\frac{n^{3}}{\ln (2)^{n}}=\frac{(n+1)^{3} \cdot \ln 4^{n}}{\ln (2)^{n+1} \cdot n^{3}}=\frac{n^{3}+3 n^{2}+3 n+1}{\frac{n^{3}}{n^{3}} \cdot \ln (2)}=\frac{1}{1} \)
\( h) \frac{n^{3}}{\ln (3)^{n}} \Rightarrow \frac{(n+1)^{3} \cdot \ln (3)^{n}}{\ln (3)^{n+1} \cdot n^{3}}=\frac{n^{3}+3 n^{2}+3 n+1}{\ln (3) \cdot n^{3}}=? \)
Text erkannt:
\( g)=\frac{n^{3}}{\ln (2)^{n}}=\frac{(n+1)^{3} \cdot \ln (2)^{4}}{\lg (2)^{n+1} \cdot n^{3}}=\frac{n^{3}+3 n^{2}+3 n+1}{n^{3} \cdot \ln (2)}=\frac{1}{1} \)
\( h) \frac{n^{3}}{\ln (3)^{n}} \Rightarrow \frac{(n+1)^{3} \cdot \ln 5^{n}}{\ln \left(3^{n+1} \cdot n^{3}\right.}=\frac{n^{3}+3 n^{2}+3 n+1}{\ln (3) \cdot n^{3}}=2 \)
Problem/Ansatz:
Ich muss die Aufgaben g und h mit dem Quotientenkriterium überprüfen. Was mache ich falsch? H müsste konvergent sein, aber verstehe nicht wieso.