Aufgabe:
Text erkannt:
6
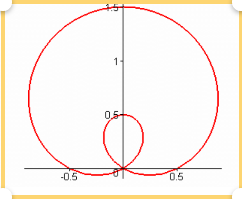
Berechnen Sie die Fläche A, die innerhalb der großen Schleife, aber außerhalb der kleinen Schleife der Kurve liegt.
r(φ)=1/2+sin(φ), 0 ≤ φ ≤ 2π
Problem/Ansatz:
Wie gehe ich bei der Aufgabe am besten vor ?
Würde man erstmal die kleine Fläche berechnen, dann die große und anschließend das voneinander abziehen ?
Ich habe das Problem die Grenzen zu setzten von wo bis wo. Formel wäre ja, \(1/2 \int\limits_{φ1}^{φ2} r^2 *d*φ \)