Hallo,
Der Beweis ist inTeil 2 der Antwort (s.u.). Hier kommt vorher
Teil 1
Folgendes sind die Ergebnisse, die ich zu dem Thema heraus gefunden habe.
Zuerst führe ich eine Punkt \(Q\) ein. \(Q\) halbiert die Strecke \(B_1C_1\) und liegt auf der Mittelparallelen durch \(M_bM_c\).
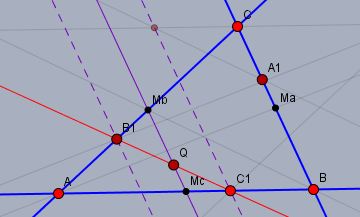
Um dies zu zeigen betrachte ich die beiden Parallelen zu \(BC\) durch die Punkte \(B_1\) und \(C_1\) (lila gestrichelt). Da \(|AC_1| \div |C_1B| = |CB_1| \div |B_1A|\) ist, hat die Parallele durch \(C_1\) den selben Abstand zu \(A\) wie die Parallele durch \(B_1\) zu \(BC\). Folglich haben beide Parallelen den gleichen Abstand zur Mittelparallelen durch \(M_bM_c\) und diese Mittelparallele ist auch Mittelparallele zu den lila gestrichelten Geraden. Somit halbiert diese Mittelparallele die Strecke \(B_1C_1\) und der Punkt \(Q\) liegt auf derselben.
Der Punkt \(A'\) sei das Spiegelbild von \(A\) an \(Q\). Und da \(Q\) auf der Mittelparallelen \(M_bM_c\) liegt, muss \(A'\) auf \(BC\) liegen. Das Viereck \(AC_1A'B_1\) ist ein Parallelogramm.
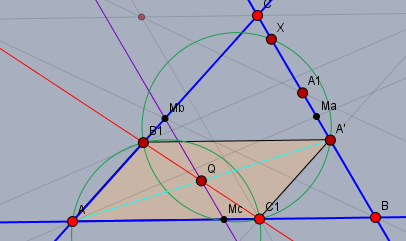
Weiter betrachte ich den Umkreis \(k\) des Dreiecks \(\triangle AC_1B_1\) und sein Spiegelbild \(k'\) an \(B_1C_1\) (beide grün). \(k'\) schneidet \(BC\) in zwei Punkten. Einer der Punkte ist zwangsläufig \(A'\), da \(A'\) sowohl auf \(BC\) als auch auf \(k'\) liegen muss. Den zweiten Punkt nenne ich \(X\).
Das nächsten Bild zeigt das Dreieck \(\triangle A_1B_1C_1\) und einige Winkel:
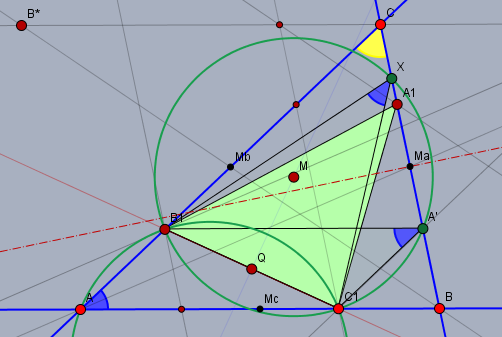
Die Winkel \(\angle BAC\), \(\angle B_1A'C_1\) und \(\angle B_1XC_1\) (blau) sind gleich, da sie Umfangswinkel in zwei Kreisen \(k\) und \(k'\) mit identischem Radius über der gemeinsamen Sehne \(B_1C_1\) sind. Es ist offensichtlich, dass es außer den Punkten \(A'\) und \(X\) keinen weiteren Punkt auf der Geraden \(BC\) gibt, von dem aus die Strecke \(B_1C_1\) unter dem Winkel \(\angle BAC\) erscheint.
Verschiebt man nun die Punkte \(A_1\) bis \(C_1\) derart, dass \(A_1\) auf \(A'\) fällt ...
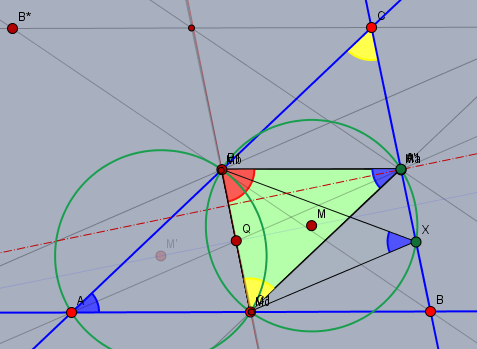
... so ist das nur möglich, wenn \(|BA_1| \div |A_1C| = 1\) ist. Das folgt aus der Forderung, dass \(B_1A'\) parallel zu \(AB\) verläuft (Parallelogramm) und somit gleichzeitig $$|AB_1|\div |B_1C| = |BA'| \div |A'C| = |BA_1| \div |A_1C| = |B_1C| \div |AB_1|$$sein muss. Es ist leicht zu zeigen, dass in diesem Fall die Dreiecke \(\triangle A_1B_1C_1\) und \(\triangle ABC\) ähnlich sind.
Verschiebt man die Punkte \(A_1\) bis \(C_1\) derart, dass \(A_1\) auf \(X\) fällt, kommt der interessantere Teil ;-)
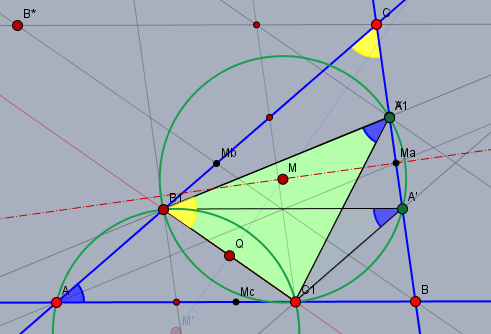
In diesem Fall ist der Winkel \(\angle C_1B_1A_1\) gleich zu \(ACB\) (beide gelb), Was noch zu beweisen wäre!
Der Mittelpunkt von \(k'\) liegt dann auf der Mittelsenkrechten von \(BC\) (rot strich-punkt). Dies muss so sein, da wegen der geforderten Verhältnisse und der Parallelität von \(B_1A'\) zu \(AB\) der Punkt \(A'\) auch das Spiegelbild von \(A_1\) an \(M_a\) ist. Fällt \(X\) mit \(A_1\) zusammen, so liegt der Mittelpunkt \(M\) von \(k'\) auf der Mittelsenkrechten der Strecke \(XA'\), die jetzt mit \(A_1A'\) zusammen fällt und somit auf der Mittelsenkrechten von \(BC\).
Teil 2: Nachtrag
Ich hatte oben schon gezeigt, dass es einen Punkt \(A'\) gibt, der einer der Schnittpunkte des Umkreises von \(\triangle A_1B_1C_1\) mit der Geraden \(BC\) ist. Fällt \(A_1\) mit \(A'\) zusammen, liegt der Trivialfall vor, für den die beiden Dreiecke ähnlich sind (s. vorletztes Bild).
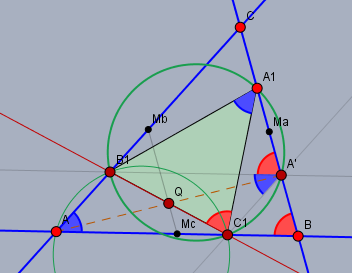
Liegt \(A_1\) nicht auf \(A'\) so gilt weiterhin, dass \(B_1A' \parallel AB\) ist und darauf folgt:$$\angle CA'B_1 = \angle CBA = \beta \quad \text{(rot)}$$und da \(\angle CA'B_1\) und \(\angle A_1C_1B_1\) beide Umfangswinkel im selben Kreis (grün) über der selben Sehne \(A_1B_1\) sind, müssen diese beiden Winkel (rot) ebenfalls gleich sein.
Zwei Dreiecke, bei denen zwei von drei Winkeln gleich sind, sind ähnlich. Somit ist \(\triangle ABC\) ähnlich zu \(A_1B_1C_1\) q.e.d.
Bem.: sollte \(A_1\) näher bei \(B\) als bei \(C\) liegen, so läuft die Argumentation über \(\gamma\) (gelb) und die Parallelität von \(A'C_1 \parallel CA\).
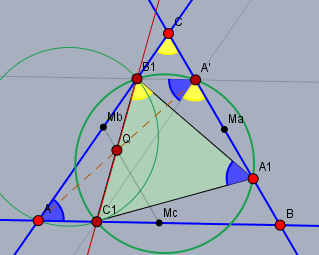
Gruß Werner