Vom Duplikat:
Titel: Zum Sinussatz. In einem Fluss liegt eine Insel mit einem Turm. Kürzeste Entfernung?
Stichworte: sinussatz,dreieck,trigonometrie,fluss,turm
Aufgabe:
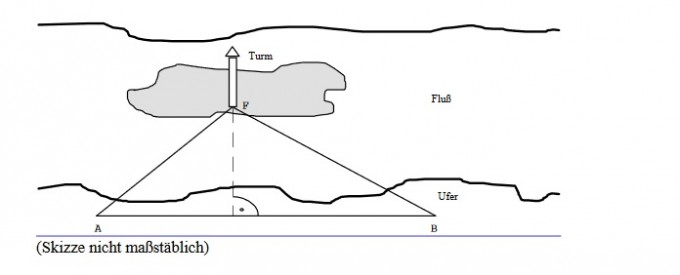
In einem Fluss liegt eine Insel mit einem Turm. Am Ufer wird eine 50m lange Strecke AB abgesteckt. Um die Entfernung des Fußpunktes F des Turmes von der Strecke AB zu bestimmen, werden die beiden Winkel BAF= α=58 grad und FBA =β = 47 grad gemessen.
a) Kontruieren Sie das Dreieck ABF in einem geeigneten Maßstab und geben Sie diesen an!
b) Berechnen Sie die kürzeste Entfernung des Fußpunktes F des Turmes von der Strecke AB!
Problem/Ansatz:
a) hätte ich das Dreicheck gezeichnet in einem Maßstab von 1:1000 weil 1cm dann ja 10meter entspricht.
b) ist der teil wo ich hilfe brauche. ich hab zwar mein tafelwerk vor mir und habe da auch formeln wie sin α =a/c aber ich hab ja nur die seite c
Als ergebnis soll 32,1m heraus kommen kann mir das jemand erklären`?