Aufgabe:
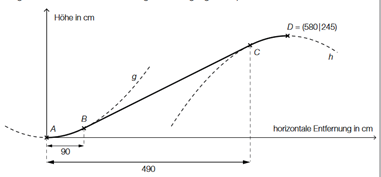
Die nachstehende Abbildung zeigt den schematischen Verlauf einer Rolltreppe. Dieser Verlauf setzt sich aus zwei Parabelstücken (Graphen der Funktionen g und h) zwischen den Punkten A und B bzw. C und D sowie einem geradlinig verlaufenden Stück zwischen den Punkten B und C zusammen. Die Übergänge in den Punkten B und C erfolgen knickfrei (Das bedeutet, dass die Funktionen an den Stellen, an denen sie zusammenstoßen, den gleichen Funktionswert und die gleiche Steigung haben.
Das heißt, die Funktionen \( g \) und h haben in den Punkten \( B \) und C dieselbe Steigung.) Bel der Ausstiegsstelle (Punkt \( D \) ) veriauft die Rolltreppe waagrecht knickfrei. Das bedeutet, dass die Funktionen an den Stellen, an denen sie zusammenstolsen, den gleichen Funktionswert und die gleiche Steigung haben.

Für die Funktion \( g \) gilt: \( g(x)=\frac{1}{360} x^{2} \)
\( x_{\text {... }} \) horizontale Entfernung von der Einstiegsstelle in cm
\( g(x) \ldots \) Hohe an der Stelle \( x \) in \( \mathrm{cm} \)
Das zwischen den Punkten \( B \) und C geradlinig verlaufende Stück kann durch die Funktionsgleichung \( f \) mit \( f(x)=\frac{1}{2} x-\frac{45}{2} \) beschrieben werden.
a) Berechnen Sie den Koeffizienten der Funkton h mit h(x)=ax²+bx+c
b) Die Fläche, die sich zwischen der Rolltreppe und dem Boden befindet (im Intervall 0;568), soll mit Farbe angestrichen werden. Überprüfen sie, ob 1 Liter Farbe ausreichend ist, wenn 1 Liter Farbe für 12 m² benötigt wird.