Vielen Dank für deine Anmerkung. Für die b) habe ich jetzt folgenden Ansatz. Ich bin mir jedoch immer noch nicht sicher, ob das so richtig ist. Könntest du drüber schauen? Mfg
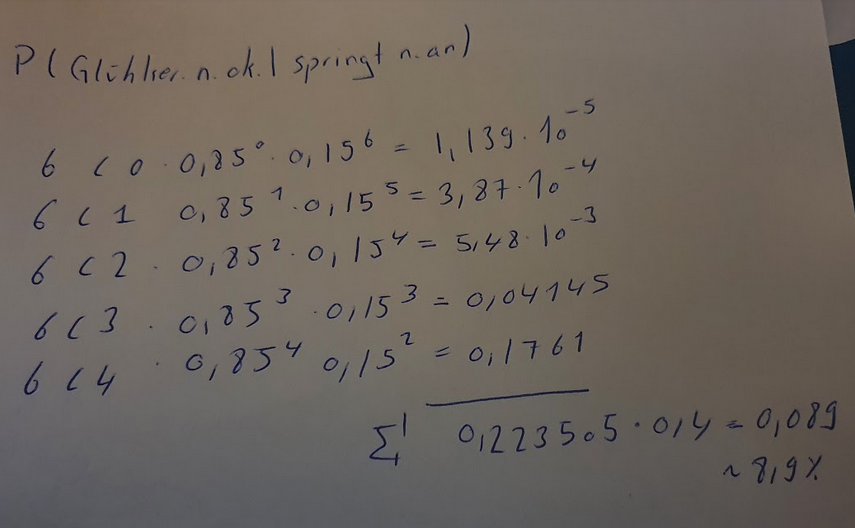
Text erkannt:
n.an)
\( 6<0.0,85^{\circ} \cdot 0,15^{6}=1,139 \cdot 10^{-5} \)
\( 6\left(110,85^{1} \cdot 0,15^{5}=3,87 \cdot 10^{-4}\right. \)
\( 6<2 \cdot 0,85^{2} \cdot 0,15^{4}=5,48 \cdot 10^{-3} \)
\( 6\left(3 \cdot 0,85^{3} \cdot 0,15^{3}=0,04145\right. \)
\( 6<4 \cdot 0,85^{4} 0,15^{2}=0,1761 \)
\( \sum \limits_{1}^{1} 0,223505 \cdot 0,4=0,089 \)
$$ 18,9 \% $$