Woher die Rechnung? Wieso??????
Ops! - ich dachte mein Bild oben reicht aus. Aber gut:
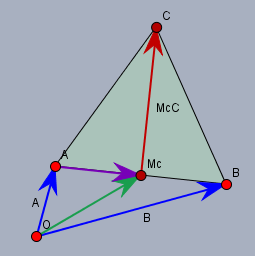
Zunächst geht es darum, bis zum Punkt \(M_c\) zu kommen. \(M_c\) liegt auf halber Strecke zwischen \(A\) und \(B\). Von \(A\) nach \(B\) geht der Vektor$$\vec{AB} = B-A$$Die Hälfte (lila) davon ist$$\frac 12 \vec {AB} = \frac12 (B-A) $$und wenn man über den Punkt \(A\) nach \(M_c\) will so ist der Ortsvektor zu \(M_c\) (grün)$$\begin{aligned}M_c &= A + \frac 12(B - A) \\&= A + \frac 12 B - \frac 12 A \\&= \frac 12 A + \frac 12 B \\&= \frac12(A + B)\end{aligned}$$Von \(M_c\) aus kann man nach \(C\) kommen. Der Vektor \(\vec{AB}^{\perp}\) (s.o. wg \(\perp\)) steht senkrecht auf \(\vec{AB}\) und ist genauso lang, also auch genauso lang wie eine Seite des gleichseitigen Dreiecks. Da die Höhe im Dreieck \(\sqrt3/2\) mal die Seitenlänge ist, ist der Vektor \(\vec{M_cC}\) (rot)$$\vec{M_cC} = \frac 12 \sqrt 3 \, \vec{AB}^{\perp}$$und wenn man die beiden addiert (grüner plus roter Vektor), kommt man zum Ortsvektor von \(C\)$$\begin{aligned} C &= M_c + \frac 12\sqrt 3\, \vec{AB}^{\perp}\\ &= \frac 12(A+B) + \frac12 \sqrt 3(B-A)^{\perp} \end{aligned}$$