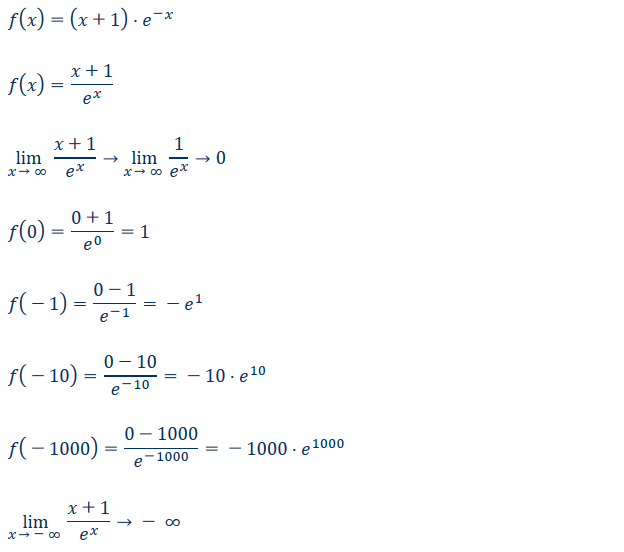
Text erkannt:
\( f(x)=(x+1) \cdot e^{-x} \)
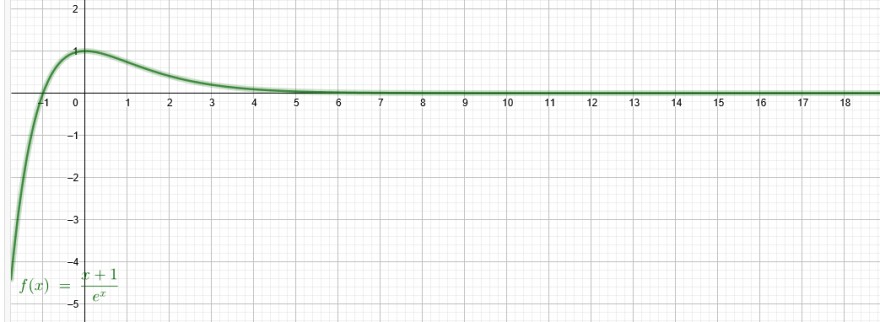
\( f(x)=\frac{x+1}{e^{x}} \)
\( \lim \limits_{x \rightarrow \infty} \frac{x+1}{e^{x}} \rightarrow \lim \limits_{x \rightarrow \infty} \frac{1}{e^{x}} \rightarrow 0 \)
\( f(0)=\frac{0+1}{e^{0}}=1 \)
\( f(-1)=\frac{0-1}{e^{-1}}=-e^{1} \)
\( f(-10)=\frac{0-10}{e^{-10}}=-10 \cdot e^{10} \)
\( f(-1000)=\frac{0-1000}{e^{-1000}}=-1000 \cdot e^{1000} \)
\( \lim \limits_{x \rightarrow-\infty} \frac{x+1}{e^{x}} \rightarrow-\infty \)