9x² -16y² -36x -128y -364 = 0
9x²-36x -16y² -128y =364
9*(x^2-4x)-16*(y^2+8y)=364
9*(x^2-4x+2^2)-16*(y^2+8y+4^2)=364+9*2^2-16*4^2=400-256
9*(x-2)^2-16*(y+4)^2=144
\( \frac{(x-2)^2}{16} \) -\( \frac{(y+4)^2}{9} \) =1
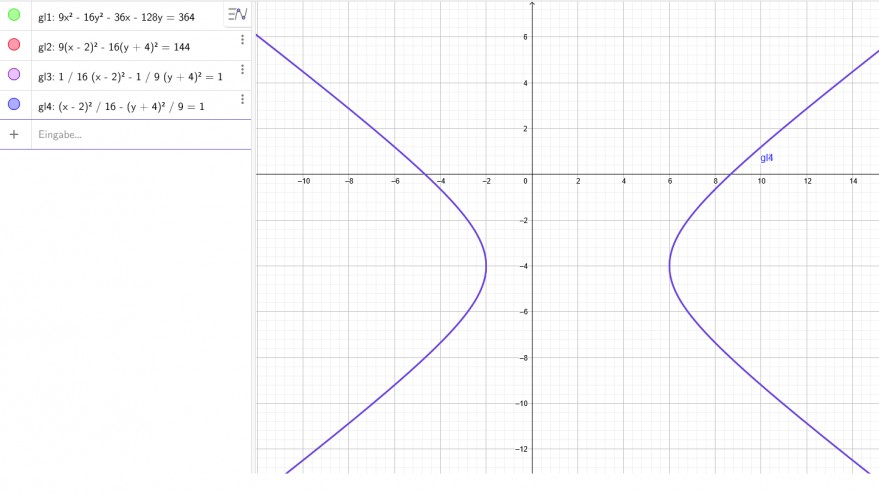
Text erkannt:
gl1: \( 9 x^{2}-16 y^{2}-36 x-128 y=364 \)
gl2:
\( \mathrm{g}^{13}: 1 / 16 \)