Partikuläre Lösung einer homogenen DGL bestimmen

Question

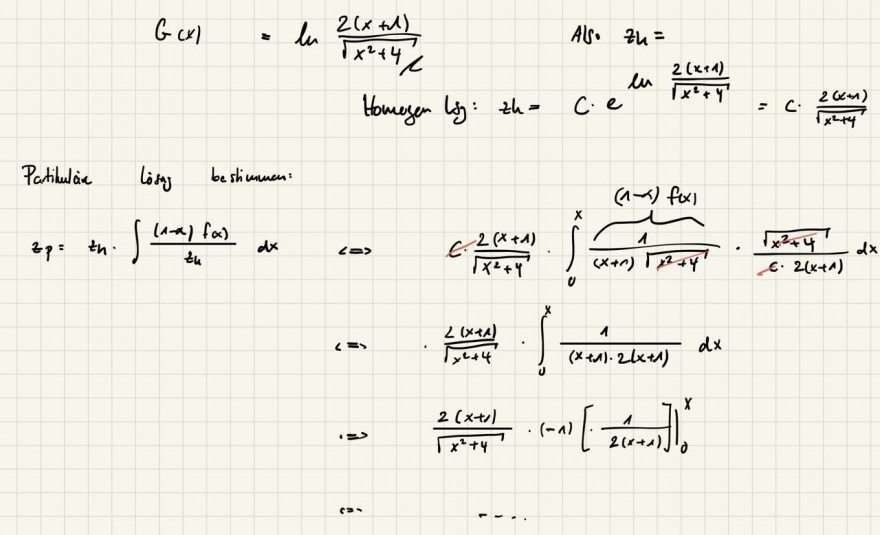
Ich versuche gerade die partikuläre Lösung einer DGL zu bestimmen.

Die homogene habe ich schon, zu sehen oben rechts im Bild, bennant zh. Nach dem einsetzten in die Formel für die partikuläre Lösung bekomme ich aber leider nicht das richtige Ergebnis aus der Musterlösung, welches arctan(x/2) lautet.

(In der ML wurde das x durch t substituiert und nach dt integriert) ( Nicht wundern, das über dem Integral (1-a) f(x) steht. Das ganze hier war ne Bernoulli DGL die homogenisiert wurde)

Meine Fragen

1. Wie komme ich auf die partikuläre Lösung?

2. In der Musterlösung wird das x in diesem Schritt sowohl in der homogenen Lösung als auch in f(x) durch ein t ersetzt und dann nach t integriert mit den Grenzen 0 bis x. Warum? Auch bei der Bestimmung von der homogenen Lösung wurde schon ohne für mich ersichtlichen Grund substituiert.

3. Warum integriere ich von 0 bis x?

Vielen Dank im Voraus.

Comments

Wir kennen die Dgl nicht!

und Variation der Konstanten hilft immer.

von 0 an integrieren wenn der anfangswert y(0) gegeben ist.

in der Schule wird  leider oft zwischen Grenzen x  und x im Integranden kein Unterschied gemacht. aber wie die Variable im Integranden heisst ist egal , oft nimmt man t oft auch ξ, aber man sollte NIE dieselbe Variable, die in den Grenzen vorkommt verwenden, denn die Grenze gibt an bis wo man integriert, das  nach was man integriert.

Gruß lul

---

Okay, danke erstmal für den Kommentar.

Die zugehörige DGL lautet:

y´ + \( \frac{(4-x)}{(3x^3+3x^2+12x+12)} \) * y - \( \frac{1}{y^2} \) * \( \frac{1}{(x+1)* sqrt(9x^2+36)} \) =0

Also wenn ein Anfangswert gegeben ist y(x) = y0, dann integriere ich immer vom gegeben x an aufwärts?

---

https://www.micbaum.y0w.de/uploads/LoesungsansaetzeDGLzweiterOrdnung.pdf

Ist in diesem Dokument (Abschnitt inhomogene lineare Differentialgleichungen) das c(x) meine partikuläre Lösung? In diversen Videos sehe ich immer, dass die partikuläre Lösung eigentlich durch zp = zh * integral ( (f(x) / zh)) dx bestimmt wird? Wenn ich aber Versuche die partikuläre Lösung durch zuvor gegebene Gleichung zu bestimmen dann kommt nicht das gleiche raus, wie wenn ich dem Vorgehen auf dem Blatt oben folge. Oder verwechsel ich da was und ist c(x) gar nicht meine partikuläre Lösung?

Answer 1

Hallo,

Antwort von Wolfram Alpha:

Mein Weg ist zwar etwas anders , aber vielleicht hilft es Dir weiter.

Comments

!! Nur um nochmal zu prüfen ob ich das richtig verstanden habe:

1. Meine homogene Lösung ist e^((integral(g(x))dx )

2. Was genau rechne ich mit Integral( s(x) * e^(Integral g(x) dx) aus? Ist das meine partikuläre Lösung? (Ich denke nicht)

3. Wann benutzt man dann die Formel für die partikuläre Lösung zp = zh * integral ( (f(x) / zh)). Hier braucht man sie ja anscheinend nicht.

4.Und in wie fern hängen Integral( s(x) * e^(Integral g(x) dx) und partikuläre Lösung zusammen, falls sie es tun?

Answer 2

Hallo

das 1/y^2  ist anders geschrieben als  y und y'  soll das eine Konstante sein oder ein Druckfehler?

wenn es einfach 1/y^2 ist dann ist das keine lineare Dgl und kann nicht in homogenen und inhomogenen Teil getrennt werden.

was diene Lösung mit dieser Dgl zu tun hat sehe ich nicht.

Gruß lul

Comments

Das 1/y^2 ist keine Konstante. Das ist eine Bernoulli-DGL, die wurde mit dem Ansatz z(x) = y(x)^(1-alpha) zu einer linearen inhomogenen DGL umgeformt. Alpha ist in diesem Fall -2 , da der Exponent von y -2 ist.

---

Danke, bleibt noch ne Frage?

lul

---

https://www.micbaum.y0w.de/uploads/LoesungsansaetzeDGLzweiterOrdnung…


Ist in diesem Dokument (Abschnitt inhomogene lineare Differentialgleichungen) das c(x) meine partikuläre Lösung? In diversen Videos sehe ich immer, dass die partikuläre Lösung eigentlich durch zp = zh * integral ( (f(x) / zh)) dx bestimmt wird? Wenn ich aber Versuche die partikuläre Lösung durch zuvor gegebene Gleichung zu bestimmen dann kommt nicht das gleiche raus, wie wenn ich dem Vorgehen auf dem Blatt oben folge. Oder verwechsel ich da was und ist c(x) gar nicht meine partikuläre Lösung?

Edit: Erst fälschlicherweise oben als Kommentar gepostet.

---

Hallo

c(x) ist nicht die partikuläre Lösung, die entsteht wenn c(x) mit der Lösung der homogenen Lösung  multipliziert wird, das ist dann die gesamte Lösung. also homogen + partikulär

Gruß lul

---

Dann müsste ich doch eigentlich bei beiden das gleiche raus bekommen oder?

hier ist natürlich zh= yh

Oder sind mein zh und e^(F(x)) falsch?

Die untere Gleichung habe ich hier her:

Wo ist der Fehler?