Steinitzscher Austauschsatz Verständnisfrage

Question

Aufgabe:

Zeigen Sie das T eine linear unabhängige Teilmenge von C³ ist und eine erzeugende Teilmenge von C³ IST

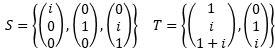
Text erkannt:

$S=\left\{\left(\begin{array}{l}i \\ 0 \\ 0\end{array}\right),\left(\begin{array}{l}0 \\ 1 \\ 0\end{array}\right),\left(\begin{array}{l}0 \\ i \\ 1\end{array}\right)\right\} \quad T=\left\{\left(\begin{array}{c}1 \\ i \\ 1+i\end{array}\right),\left(\begin{array}{l}0 \\ 1 \\ i\end{array}\right)\right\}$

Text erkannt:

$S=\left\{\left(\begin{array}{l}i \\ 0 \\ 0\end{array}\right),\left(\begin{array}{l}0 \\ 1 \\ 0\end{array}\right),\left(\begin{array}{l}0 \\ i \\ 1\end{array}\right)\right\} \quad T=\left\{\left(\begin{array}{c}1 \\ i \\ 1+i\end{array}\right),\left(\begin{array}{l}0 \\ 1 \\ i\end{array}\right)\right\}$

Verwenden sie den Algorithmus im Steinitzschen Austauschsatz um zwei Elemente von S durch die Elemente von T zu auszutauschen

Problem/Ansatz:

1) Bei der linearen Unabhängigkeit prüfe ich da einfach ob ich mit beliebigen Skalaren für die Elemente aus T einen Nullvektor bauen kann, also einfach Skalare null setzen?

2) erzeugende Teilmenge: Hier ist es ja so ob man mit Skalaren vor jedem Element aus S alle Vektoren aus C³ bauen kann, aber da würde ja in der 3. Zeile das i fehlen? da ist nur in 3.Vektor unten eine 1 und wäre dann ja C,C,R und nicht C³

3) Bei dem steinitzschen Austauschsatz tu ich mir schwer zu verstehen nach was ich gehen muss und was da ausgetauscht werden soll und welchen Zweck dies hat.

Wäre für Hilfe dankbar. Erklärvideos zu Steinitz im Internet halfen mir da auch nicht weiter

VG coffee.cup

Answer 1

also einfach Skalare null setzen?

Dann bekommst du 0.

Immer.

Dann wäre alles linear unabhängig.

Dann könnte man sich die Definition sparen.

Die Vektoren $v_1,\dots,v_n$ sind linear unabhängig wenn die Gleichung

        $\alpha_1v_1 + \dots + \alpha_n v_n = 0$

keine weiteren Lösungen als die von dir angesprochene hat. Bestimme also die Lösungsmenge dieser Gleichung.

aber da würde ja in der 3. Zeile das i fehlen?

Die Skalare kommen aus $\mathbb{C}$. Damit kannst du dir in der 3. Zeile ein $\mathrm{i}$ basteln.

Falls in der Aufgabe nichts anderes steht, dann kommen die Skalare des Vektorraumes $K^n$ aus dem Körper $K$.

Comments

okay, danke, das hilft mir weiter.

Wie stelle ich das danach mit dem Austauschsatz an?

---

In der Basis $S = \{v_1,v_2,v_3\}$ soll ein Vektor durch $w$ ersetzt werden.

Löse dazu die Gleichung

        $\alpha_1v_1 + \alpha_2v_2 + \alpha_3v_3 = w$.

Ersetze in $S$ einen Vektor $v_i$, dessen Koeffizient $\alpha_i$ ungleich $0$ ist, durch $w$.