Hallo Roland,
von Vorteil ist, wenn man erkennt, dass $$2^2+3^3=13 \\ 1^2+4^2 = 17 \\ 2^2+4^2= 20$$ist. D.h. jede Seite jedes Quadrats lässt sich als Länge zwischen zwei Gitterpunkten eines Koordinatensystems darstellen.
Man beginnt mit einem kariertem Papier und markiert links unten den Ursprung. Die Punkte \(C\) und \(D\) setzt man auf die Koordinaten \(C=(2|\,0)\) und \(B=(0|\,3)\). Somit ist \(|BC| = \sqrt{13}\)
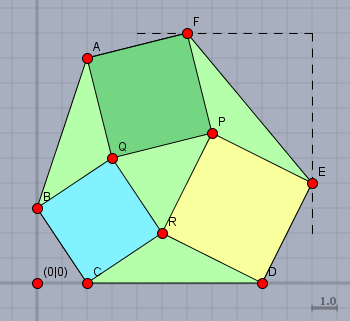
Darüber konstruiert man das erste (blaue) Quadrat. Der Punkt \(R\) wird zwangsläufig zu \(R=(5|\,2)\). Punkt \(D\) bekommt die Koordinate \(D=(9|\,0)\). So ist \(|RD|=\sqrt{20}\), und die Lage des gelben Quadrats mit der Fläche \(20\,\text{cm}^2\) liegt fest. usw.
Die Fläche bekommt man durch Auszählen der Kästchen, mit Hilfe der Gaußschen Flächenformel oder man zieht vom umhüllenden Rechteck \(F_R=110\,\text{cm}^2\) die freien Flächen wieder ab.$$F = 110 - (\underbrace{4+ 15}_{\text{rechts}}) - (\underbrace{3+10}_{\text{links}}) = 78$$
Gruß Werner