Hallo
(i)
(dP)/(dt) = (cos t - (2t) / (1 + t^2)) P(t)
1/P dP = cos t dt - (2t) / (1 + t^2) dt
∫1/P dP = ∫cos t dt - ∫(2t) / (1 + t^2) dt
-------------------------------------------------
Nebenrechnung
Substitution: u = 1 + t^2
(du)/(dt) = 2t
du = 2t dt
∫(2t) / (1 + t^2) dt =
∫(2t) / u dt =
∫ 1/u du
-------------------------------------------------
∫1/P dP = ∫cos t dt - ∫ 1/u du
ln P + C1 = sin t + C2 - ln u + C3 | Resubstitution: u = 1 + t^2
ln P + C1 = sin t + C2 - ln(1 + t^2) + C3
ln P = sin t - ln(1 + t^2) + C4 | C4 = C2 + C3 - C1
P(t) = esin t - ln(1 + t^2) + C4
P(0) = e^C4 = P0
P(t) = esin t - ln(1 + t^2) + C4
P(t) = eC4 esin t - ln(1 + t^2)
P(t) = P0 esin t - ln(1 + t^2)
(ii)
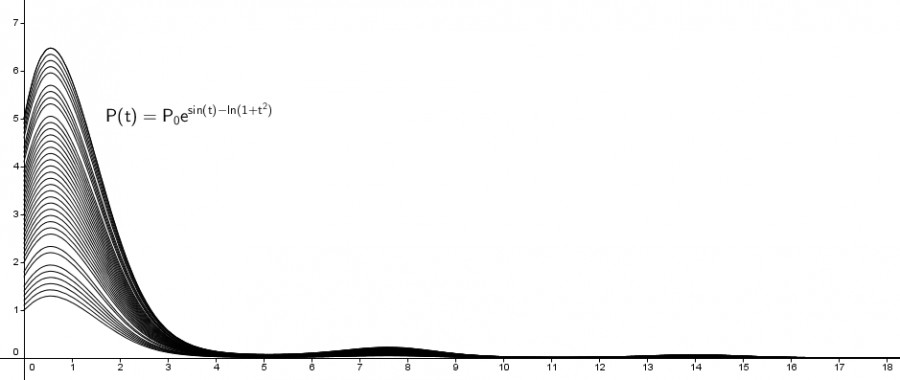
Gleich nach dem Beginn der Behandlung nimmt die Stärke des Pilzbefalls bis auf
einen Höchstwert zu, nach dem Erreichen des Höchstwertes nimmt die Stärke ab und geht gegen 0.
Verlauf des Graphen für verschiedene Anfangswerte P0, von P0 = 1 bis P0 = 5.
(iii)
P(3) = P0 esin 3 - ln(1 + 3^2)
P(3) ≈ 0,11 P0
Drei Monate nach Behandlungsbeginn ist die Stärke des Pilzbefalls auf ungefähr ein Zehntel des Anfangswerts P0 abgeklungen.